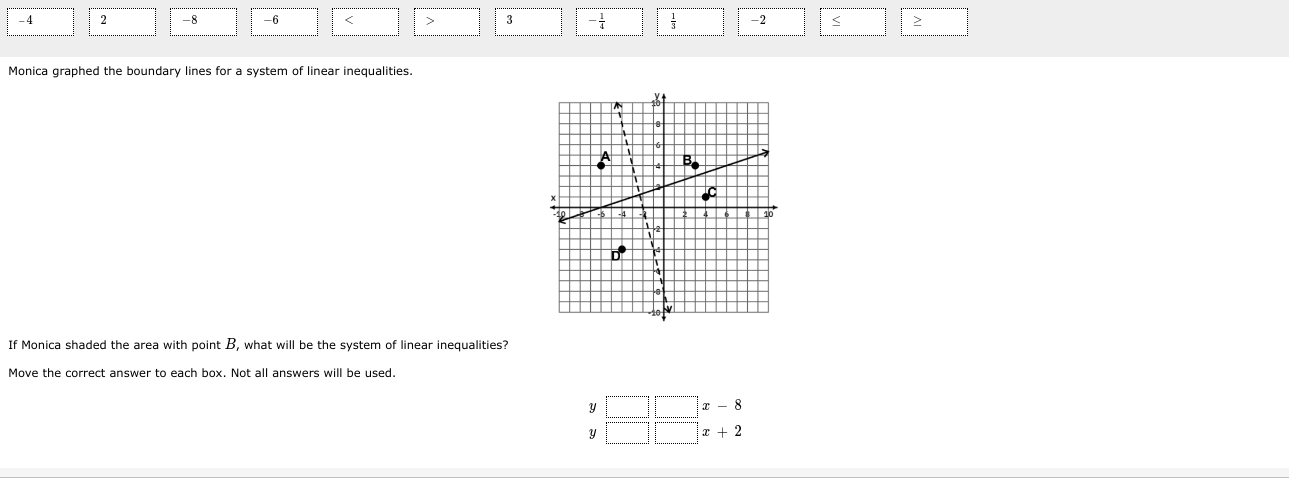
If Monica shaded the area with point B, what will be the system of linear inequalities?
Understand the Problem
The question is asking for the system of linear inequalities that corresponds to a graph where a specific area indicated by point B is shaded. We need to identify the correct inequalities based on the graph provided.
Answer
The system of linear inequalities is: $$ y \geq 2x - 4 \text{ and } x \geq -2 $$
Answer for screen readers
The system of linear inequalities is: $$ y \geq 2x - 4 \quad \text{and} \quad x \geq -2 $$
Steps to Solve
-
Identify the Boundary Lines
From the graph, we can see two boundary lines. The equations of the lines can be derived from points A and C:
- For line AC, it passes through points A (3, 2) and C (5, 6).
- The slope $m$ can be calculated as: $$ m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{6 - 2}{5 - 3} = \frac{4}{2} = 2 $$
- Using point-slope form, the equation is: $$ y - 2 = 2(x - 3) \implies y = 2x - 4 $$
-
Determine the Shading of the Area
The area shaded corresponds to the inequality formed by the line:
- Since point B (4, 4) lies above the boundary line, the inequality for line AC is: $$ y \geq 2x - 4 $$
-
Identify the Other Boundary Line
The other line appears to be a vertical boundary produced by points D and B. This line is defined along $x = -2$:
- The inequality for this line, considering that the shaded area is to the right of it, is: $$ x \geq -2 $$
-
Form the System of Inequalities
We combine the inequalities based on the shaded regions above:
- The corresponding system of inequalities is: $$ y \geq 2x - 4 \quad \text{and} \quad x \geq -2 $$
The system of linear inequalities is: $$ y \geq 2x - 4 \quad \text{and} \quad x \geq -2 $$
More Information
This answer describes the conditions for the shaded area in the graph corresponding to the two inequalities derived from the lines. The nature of the inequalities indicates which regions are included or excluded based on the boundaries, with a "greater than or equal to" corresponding to areas above the line.
Tips
- Misidentifying the direction of the inequality based on point location relative to the line.
- Forgetting to check both boundary lines when determining the system of inequalities.