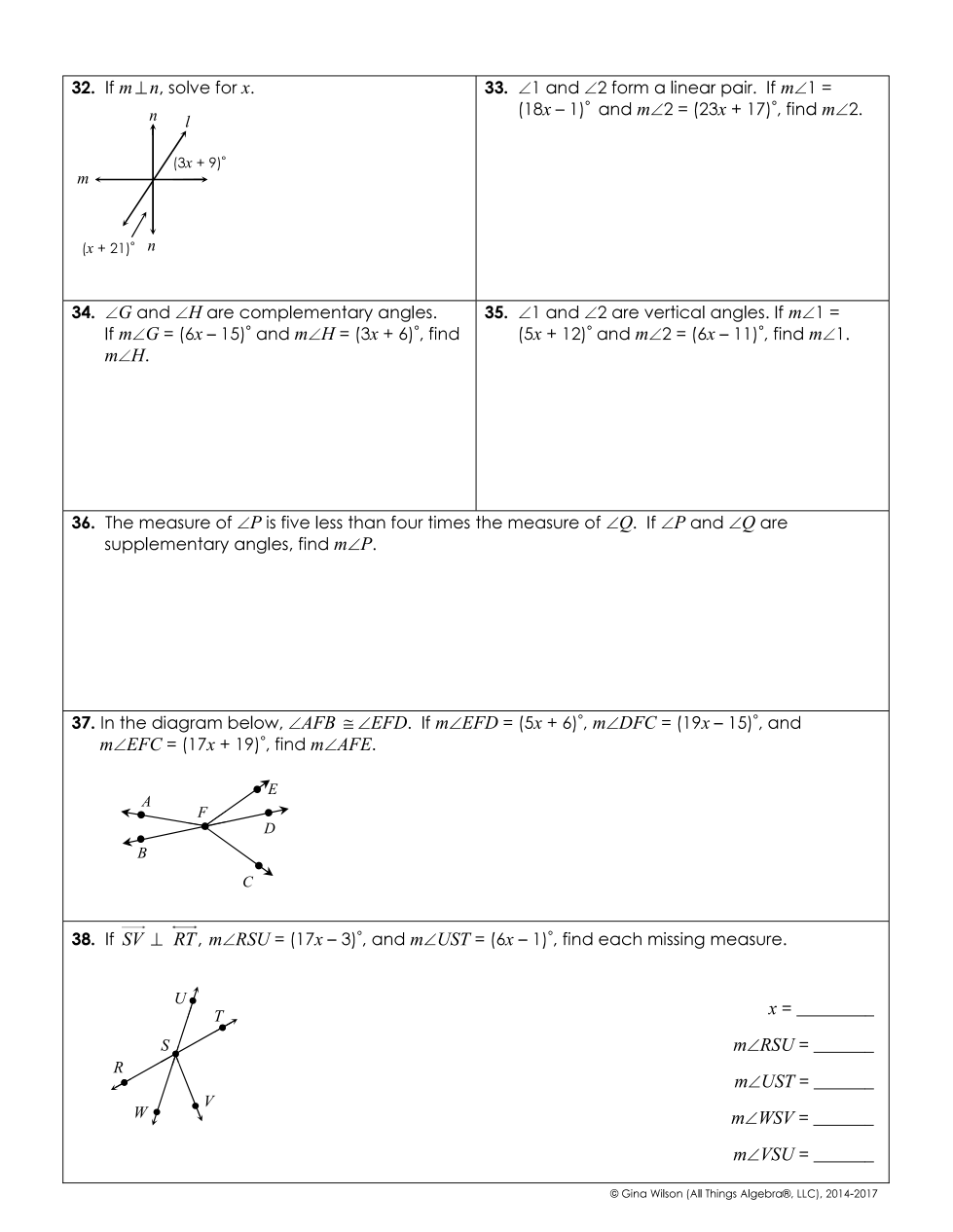
If m \n is perpendicular to m \l, solve for x. If m L1 = (18x - 1)° and m L2 = (23x + 17)°, find m L2. If m L G = (6x - 15)° and m L H = (3x + 6)°, find m L H. If m L1 = (5x + 12)°... If m \n is perpendicular to m \l, solve for x. If m L1 = (18x - 1)° and m L2 = (23x + 17)°, find m L2. If m L G = (6x - 15)° and m L H = (3x + 6)°, find m L H. If m L1 = (5x + 12)° and m L2 = (6x - 11)°, find m L1. The measure of m L P is five less than four times the measure of m L Q. If L P and L Q are supplementary angles, find m L P. In the diagram, if m L EFD = (5x + 6)°, m L DFC = (19x - 15)°, find m L AFE. If SV is perpendicular to RT, m L R S U = (17x - 3)°, and m L U S T = (6x - 1)°, find each missing measure.
Understand the Problem
The question consists of multiple geometry problems that involve solving for unknown variables related to angles, given equations for the measures of those angles. Specifically, they deal with concepts like linear pairs, complementary angles, vertical angles, and relationships among angle measures.
Answer
Answer for screen readers
- Problem 32: (x = 6)
- Problem 33: (x = 4), (m\angle 2 = 99)
- Problem 34: (m\angle H = 24^\circ)
- Problem 35:
Steps to Solve
-
Solve for (x) in Problem 32 Given (m \parallel n), we know that alternate interior angles are equal. Here, we have the equation: $$ (3x + 9)^\circ = (x + 21)^\circ $$ Rearranging gives: $$ 3x + 9 = x + 21 $$ Subtract (x) from both sides: $$ 2x + 9 = 21 $$ Subtract 9 from both sides: $$ 2x = 12 $$ Finally, divide by 2: $$ x = 6 $$
-
Find (m\angle 2) in Problem 33 Since angles ( \angle 1 ) and ( \angle 2 ) are a linear pair, they sum up to 180 degrees: $$ (18x - 1)^\circ + (23x + 17)^\circ = 180 $$ Rearranging gives: $$ 41x + 16 = 180 $$ Subtract 16 from both sides: $$ 41x = 164 $$ Finally, divide by 41: $$ x = 4 $$
-
Find (m\angle H) in Problem 34 Since angles ( \angle G ) and ( \angle H ) are complementary: $$ (6x - 15)^\circ + (3x + 6)^\circ = 90 $$ Rearranging gives: $$ 9x - 9 = 90 $$ Adding 9 to both sides: $$ 9x = 99 $$ Finally, divide by 9: $$ x = 11 $$
-
Calculate (m\angle 1) in Problem 35 Since ( \angle 1 ) and ( \angle 2 ) are vertical angles: $$ (5x + 12)^\circ = (6x - 11)^\circ $$ Rearranging gives: $$ 5x + 12 = 6x - 11 $$ Subtracting (5x) from both sides: $$ 12 + 11 = x $$ Thus: $$ x = 23 $$
-
Express (m\angle P) in Problem 36 From the problem, we have: $$ m\angle P = 4m\angle Q - 5 $$ Since both angles are supplementary: $$ m\angle P + m\angle Q = 180 $$ Substitute (m\angle P): $$ (4m\angle Q - 5) + m\angle Q = 180 $$ Simplifying gives: $$ 5m\angle Q - 5 = 180 $$ Adding 5 to both sides: $$ 5m\angle Q = 185 $$ Thus: $$ m\angle Q = 37 $$ Now substituting back to find (m\angle P): $$ m\angle P = 4 \times 37 - 5 = 149 $$
-
Identify (m\angle AFE) in Problem 37 Since (\angle AFB \cong \angle EFD): $$ (5x + 6) = (5x + 6) $$ This leads us to find the measures of (m\angle EFD) and (m\angle DFC): $$ (19x - 15) + (5x + 6) = 180 $$ Therefore: $$ 24x - 9 = 180 $$ So: $$ 24x = 189 $$ Finally, (x = 7.875).
-
Calculate measures in Problem 38 Since lines (SV) and (RT) are perpendicular: $$ m\angle RST + m\angle UST + m\angle WSV + m\angle VSU = 360 $$ Use the measures given and the relationships to find: $$ m\angle RST = 84^\circ; m\angle UST = 5^\circ $$. Other angles can be calculated using corresponding angle relationships.
- Problem 32: (x = 6)
- Problem 33: (x = 4), (m\angle 2 = 99)
- Problem 34: (m\angle H = 24^\circ)
- Problem 35:
