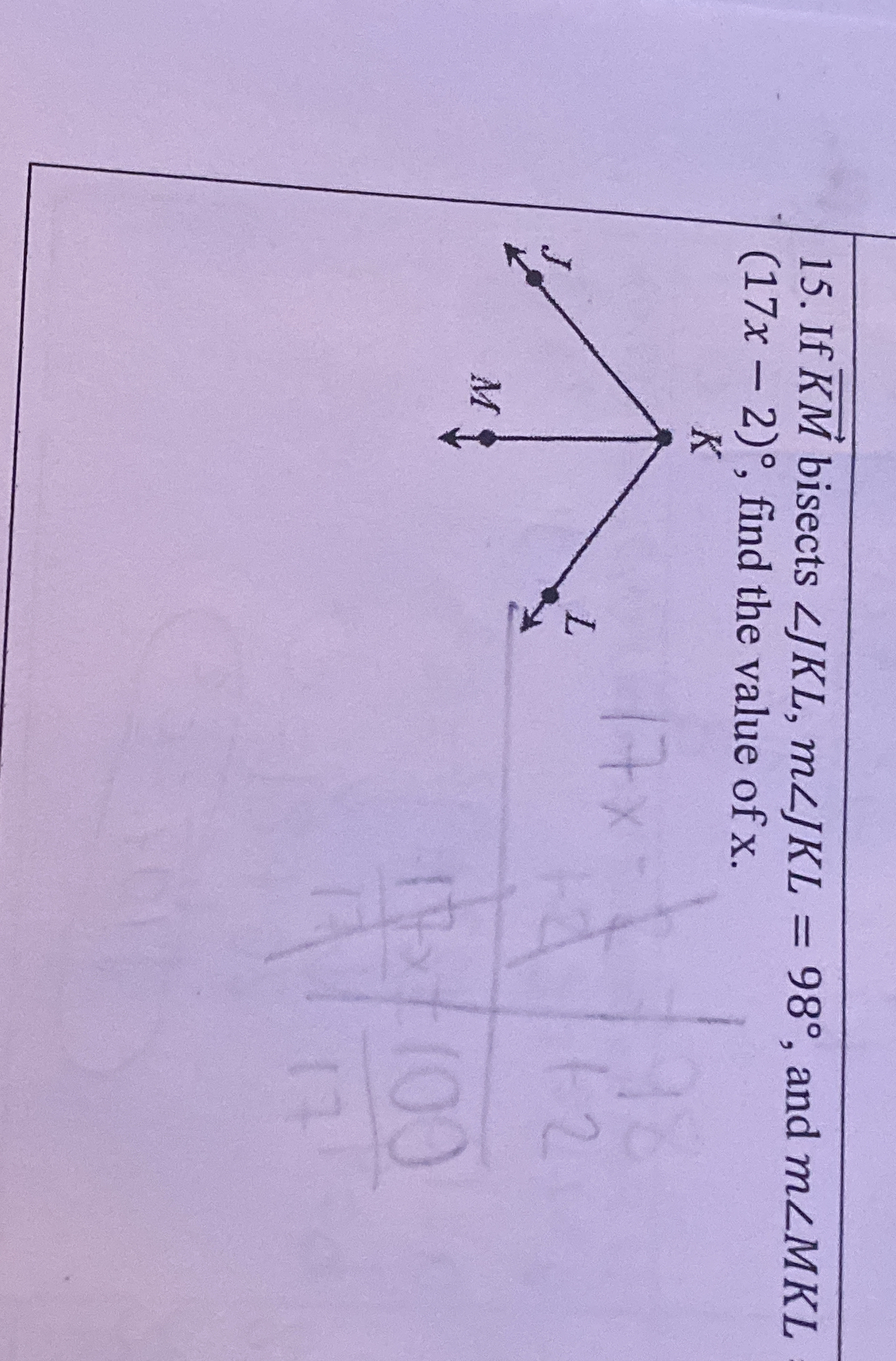
If KM bisects <JKL, m<J/KL = 98°, find the value of x.
Understand the Problem
The question is asking us to find the value of x based on the angles formed by the bisector KM, which divides the angle <JKL. We know that one angle measures (17x - 2)° and the other measures 98°. Since KM bisects <JKL, we can set up an equation to solve for x.
Answer
$$ x \approx 5.88 $$
Answer for screen readers
$$ x \approx 5.88 $$
Steps to Solve
-
Understand the relationship between angles Since KM bisects the angle <JKL, we know that it divides it into two equal parts. Therefore, we can write: $$ m<JMK = m<MKL $$
-
Set up the equation Given that one of the angles is $(17x - 2)°$ and the other angle is $98°$, we can set up the equation: $$ 17x - 2 = 98 $$
-
Solve for x Add 2 to both sides of the equation to isolate the term with x: $$ 17x - 2 + 2 = 98 + 2 $$ This simplifies to: $$ 17x = 100 $$
-
Divide to find x Now, divide both sides by 17 to solve for x: $$ x = \frac{100}{17} $$
-
Calculate the value Perform the division to find the numerical value of x: $$ x \approx 5.88 $$
$$ x \approx 5.88 $$
More Information
The value of x is approximately 5.88, which indicates how much the angle measures in relation to its expression. This shows how algebra can solve problems involving angles and their relationships in geometry.
Tips
- Incorrect equation setup: Failing to recognize that the two angles are equal leads to setting up the wrong equation. Always double-check the relationship of bisected angles.
- Calculation errors: Mistakes when adding, subtracting, or dividing can easily occur. It's important to perform calculations step-by-step carefully.
AI-generated content may contain errors. Please verify critical information