If KM bisects angle JKL, m∠JKL = 98°, and m∠MKL = (17x - 2)°, find the value of x.
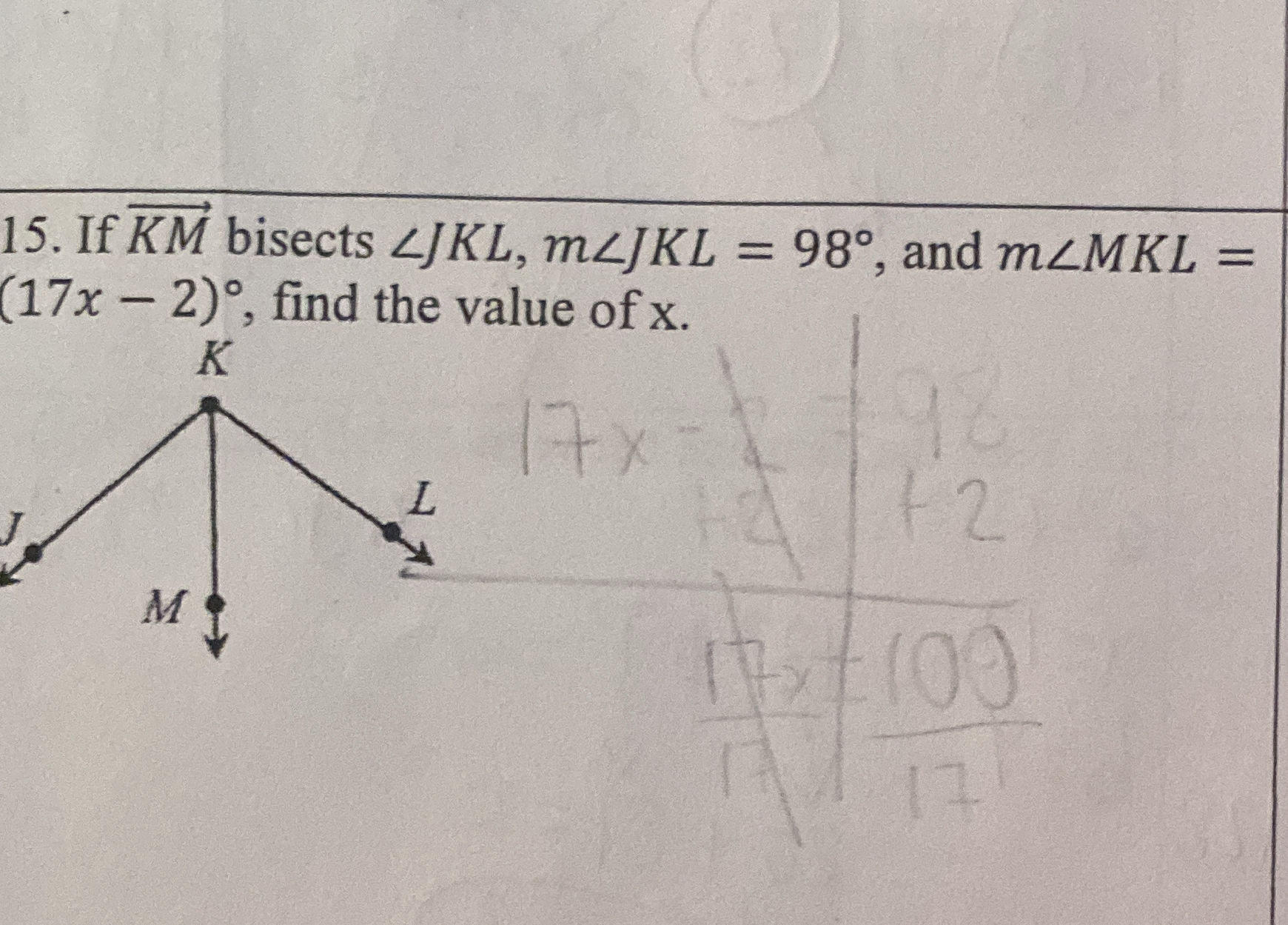
Understand the Problem
The question asks to find the value of x using the information about the angles formed by the line segments. It states that KM bisects angle JKL, provides the measure of angle JKL as 98°, and gives the measure of angle MKL as (17x - 2)°. Since KM is a bisector, we know that angle JKL is divided into two equal angles, so we can set up an equation to solve for x.
Answer
The value of \( x \) is \( 3 \).
Answer for screen readers
The value of ( x ) is ( 3 ).
Steps to Solve
-
Identify the relationship due to the bisector Since KM bisects angle JKL, we know that: $$ m∠JKM = m∠MKL = \frac{m∠JKL}{2} $$
-
Calculate the measure of the angles Given that $m∠JKL = 98°$, we find: $$ m∠JKM = m∠MKL = \frac{98°}{2} = 49° $$
-
Set up the equation We know that: $$ m∠MKL = 17x - 2 $$ So, we can set up the equation: $$ 17x - 2 = 49 $$
-
Solve for x Add 2 to both sides: $$ 17x = 49 + 2 $$ $$ 17x = 51 $$
Now, divide both sides by 17: $$ x = \frac{51}{17} $$
- Calculate the value of x Perform the division: $$ x = 3 $$
The value of ( x ) is ( 3 ).
More Information
This problem demonstrates the concept of angle bisectors and how they split angles into two equal parts. The calculation involved basic algebra to isolate the variable ( x ).
Tips
- Neglecting the division: Some might forget to divide by 2 after setting up that the angles are equal.
- Incorrect equation setup: It’s crucial to set the equation as ( 17x - 2 = 49 ) instead of mixing the angles.
AI-generated content may contain errors. Please verify critical information