If A = {x ∈ R : 4x^2 = 2x + 3} B = {x ∈ R : log(x^2) = (log(x))^2} find A ∩ B
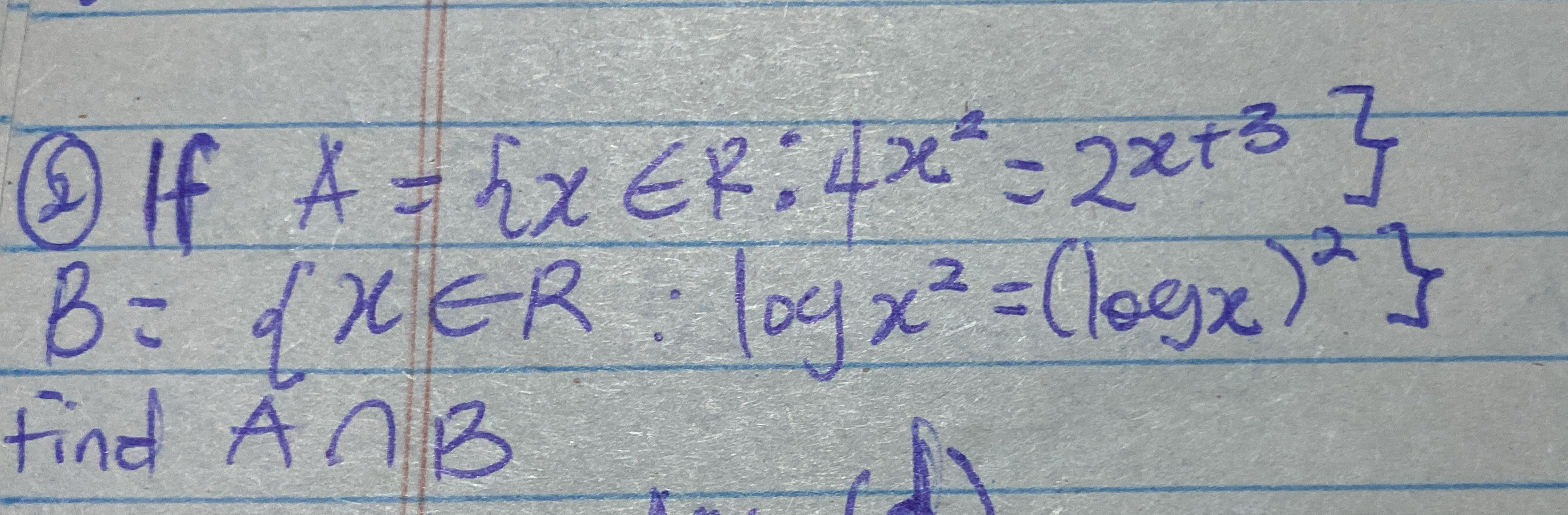
Understand the Problem
The question asks to find the intersection of two sets, A and B, defined by specific mathematical expressions.
Answer
The intersection $A \cap B$ contains the positive roots of $4x^2 - 2x - 3 = 0$.
Answer for screen readers
The intersection set $A \cap B$ includes the positive solutions from Set A, which can be computed numerically.
Steps to Solve
-
Define the Sets A and B
The set $A$ is defined by the equation: $$ 4x^2 = 2x + 3 $$ Rearranging gives: $$ 4x^2 - 2x - 3 = 0 $$
The set $B$ is defined by the equation: $$ \log(x^2) = (\log x)^2 $$ This can be rewritten using properties of logarithms.
-
Solve for Set A
To find the roots of the quadratic equation from Set A:
- Use the quadratic formula: $$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$ where $a = 4$, $b = -2$, and $c = -3$.
-
Calculate the Discriminant
Calculate the discriminant: $$ D = b^2 - 4ac = (-2)^2 - 4(4)(-3) = 4 + 48 = 52 $$
-
Find the Roots of Set A
Using the quadratic formula: $$ x = \frac{-(-2) \pm \sqrt{52}}{2(4)} = \frac{2 \pm 2\sqrt{13}}{8} = \frac{1 \pm \frac{\sqrt{13}}{2}}{4} $$ The roots are: $$ x_1 = \frac{1 + \sqrt{13}/2}{4} \quad \text{and} \quad x_2 = \frac{1 - \sqrt{13}/2}{4} $$
-
Solve for Set B
For Set B, rearranging gives: $$ \log(x^2) = 2 \log x $$ This simplifies to: $$ 2 \log x = 2 \log x $$ The values of $x$ that satisfy this equation (excluding non-positive $x$) are where $x > 0$.
-
Find the Intersection A ∩ B
Now, find the intersection of Set A and Set B. Since Set B consists only of positive $x$, check if the solutions from Set A are positive:
- Calculate the numerical values of $x_1$ and $x_2$ to check which satisfy $x > 0$.
The intersection set $A \cap B$ includes the positive solutions from Set A, which can be computed numerically.
More Information
Using numerical approximations, you can find the specific values of $x_1$ and $x_2$.
Tips
- Forgetting to check if roots are positive when dealing with logarithms.
- Misapplying the quadratic formula due to incorrect values of $a$, $b$, or $c$.
AI-generated content may contain errors. Please verify critical information