If A = {x ∈ ℝ : 4x² = 2x + 3} B = {x ∈ ℝ : log x² = (log x)²} find A ∩ B
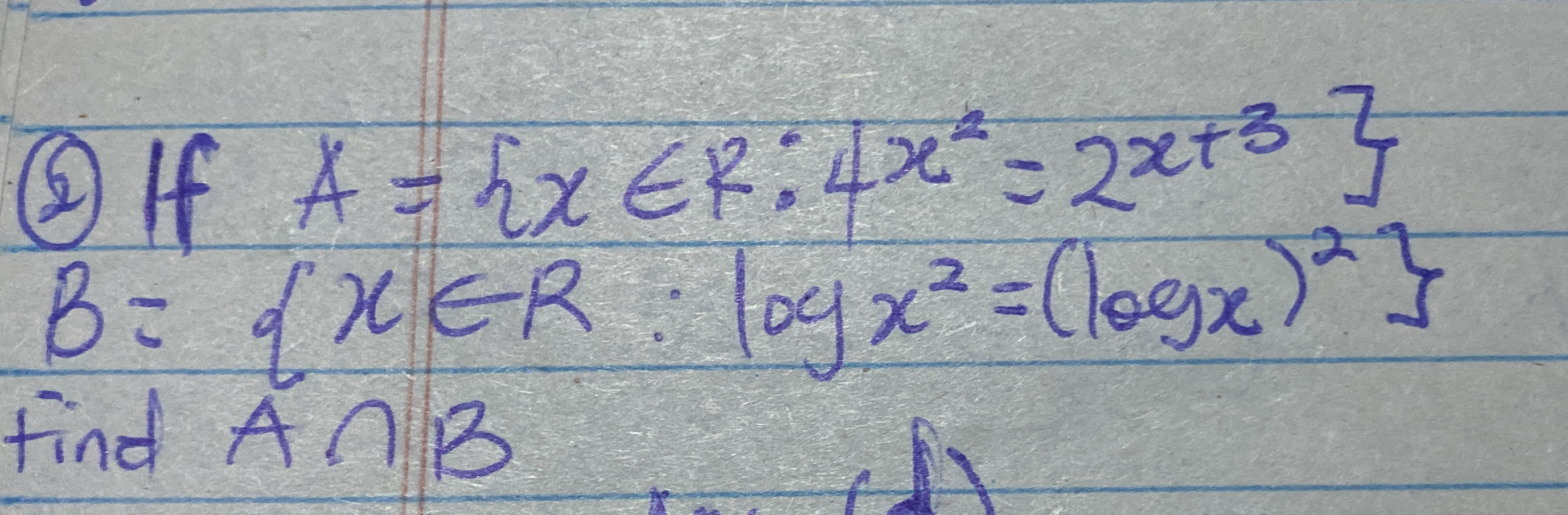
Understand the Problem
The question is asking to find the intersection of two sets, A and B, where set A is defined by a specific linear equation and set B by a logarithmic expression. This involves determining which elements belong to both sets based on their mathematical definitions.
Answer
The intersection is \( A \cap B = \{ 1 \} \).
Answer for screen readers
The intersection of sets A and B is:
$$ A \cap B = { 1 } $$
Steps to Solve
- Solve the equation for set A
We begin with the equation for set A:
$$ 4x^2 = 2x + 3 $$
Rearranging it, we get:
$$ 4x^2 - 2x - 3 = 0 $$
Using the quadratic formula ( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} ) where ( a = 4, b = -2, c = -3 ):
$$ b^2 - 4ac = (-2)^2 - 4(4)(-3) = 4 + 48 = 52 $$
Now we can find the roots:
$$ x = \frac{2 \pm \sqrt{52}}{2 \cdot 4} = \frac{2 \pm 2\sqrt{13}}{8} = \frac{1 \pm \sqrt{13}}{4} $$
So, the solutions for set A are:
$$ A = \left{ \frac{1 + \sqrt{13}}{4}, \frac{1 - \sqrt{13}}{4} \right} $$
- Solve the logarithmic equation for set B
For set B, we have:
$$ \log x^2 = (\log x)^2 $$
Rewriting it gives:
$$ 2\log x = (\log x)^2 $$
Let's set ( y = \log x ). Then we have:
$$ 2y = y^2 $$
Rearranging leads to:
$$ y^2 - 2y = 0 $$
Factoring gives:
$$ y(y - 2) = 0 $$
Thus, ( y = 0 ) or ( y = 2 ).
Returning to the variable ( x ):
- For ( y = 0 ):
$$ \log x = 0 \Rightarrow x = 10^0 = 1 $$
- For ( y = 2 ):
$$ \log x = 2 \Rightarrow x = 10^2 = 100 $$
So, the solutions for set B are:
$$ B = { 1, 100 } $$
- Find the intersection ( A \cap B )
We now need to find common elements in sets A and B.
Set A has:
$$ A = \left{ \frac{1 + \sqrt{13}}{4}, \frac{1 - \sqrt{13}}{4} \right} $$
Set B has:
$$ B = { 1, 100 } $$
Calculating ( \frac{1 + \sqrt{13}}{4} ) approximately:
$$ \sqrt{13} \approx 3.605 $$ $$ \frac{1 + 3.605}{4} \approx \frac{4.605}{4} \approx 1.15125 $$
Calculating ( \frac{1 - \sqrt{13}}{4} ) approximately:
$$ \frac{1 - 3.605}{4} \approx \frac{-2.605}{4} \approx -0.65125 $$
Since ( A ) contains elements approximately ( 1.15125 ) and ( -0.65125 ) while ( B ) contains ( 1 ) and ( 100 ), the only common member is:
$$ 1 \in B $$
Thus, the intersection ( A \cap B = { 1 } $$
The intersection of sets A and B is:
$$ A \cap B = { 1 } $$
More Information
The result indicates that the number 1 is the only solution that satisfies both the quadratic equation in set A and the logarithmic condition in set B. This demonstrates a scenario where different types of functions may intersect at specific points.
Tips
Some common mistakes include:
- Not rearranging the equations correctly before applying the quadratic formula.
- Confusing the properties of logarithms, such as forgetting that ( \log x^2 = 2 \log x ).
- Overlooking that for logarithmic equations, ( x ) must be positive, as the logarithm is not defined for non-positive numbers.
AI-generated content may contain errors. Please verify critical information