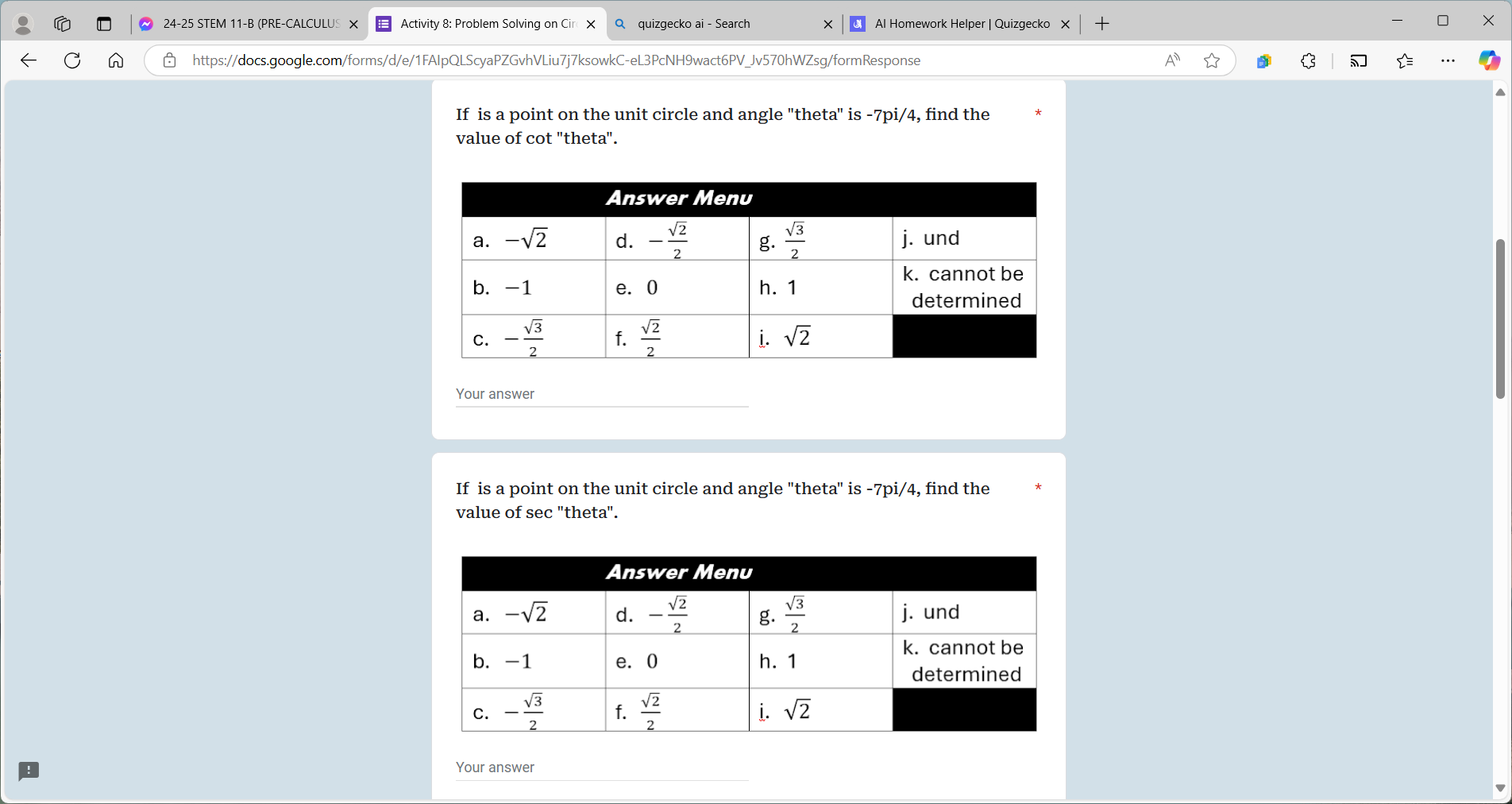
If a point is on the unit circle and the angle 'theta' is -7pi/4, find the value of cot 'theta'. If a point is on the unit circle and angle 'theta' is -7pi/4, find the value of sec... If a point is on the unit circle and the angle 'theta' is -7pi/4, find the value of cot 'theta'. If a point is on the unit circle and angle 'theta' is -7pi/4, find the value of sec 'theta'. Read more

Steps to Solve

1. Determine the angle on the unit circle

To find the corresponding angle of $-\frac{7\pi}{4}$ on the unit circle, we can add $2\pi$ (which is the same as $\frac{8\pi}{4}$) to get a positive angle:

$$ -\frac{7\pi}{4} + 2\pi = -\frac{7\pi}{4} + \frac{8\pi}{4} = \frac{\pi}{4} $$

So, the angle is $\frac{\pi}{4}$.

2. Identify coordinates on the unit circle

The coordinates of the angle $\frac{\pi}{4}$ (in radians) on the unit circle are

$$ \left( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right) $$

3. Calculate cotangent

The cotangent of an angle is defined as the ratio of the adjacent side to the opposite side, or

$$ \cot(\theta) = \frac{\cos(\theta)}{\sin(\theta)} $$

For $\frac{\pi}{4}$,

$$ \cot\left(\frac{\pi}{4}\right) = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = 1 $$

4. Calculate secant

The secant of an angle is defined as the reciprocal of the cosine:

$$ \sec(\theta) = \frac{1}{\cos(\theta)} $$

For $\frac{\pi}{4}$,

$$ \sec\left(\frac{\pi}{4}\right) = \frac{1}{\frac{\sqrt{2}}{2}} = \sqrt{2} $$