Rationalize and simplify $\frac{3}{\sqrt{2}}$
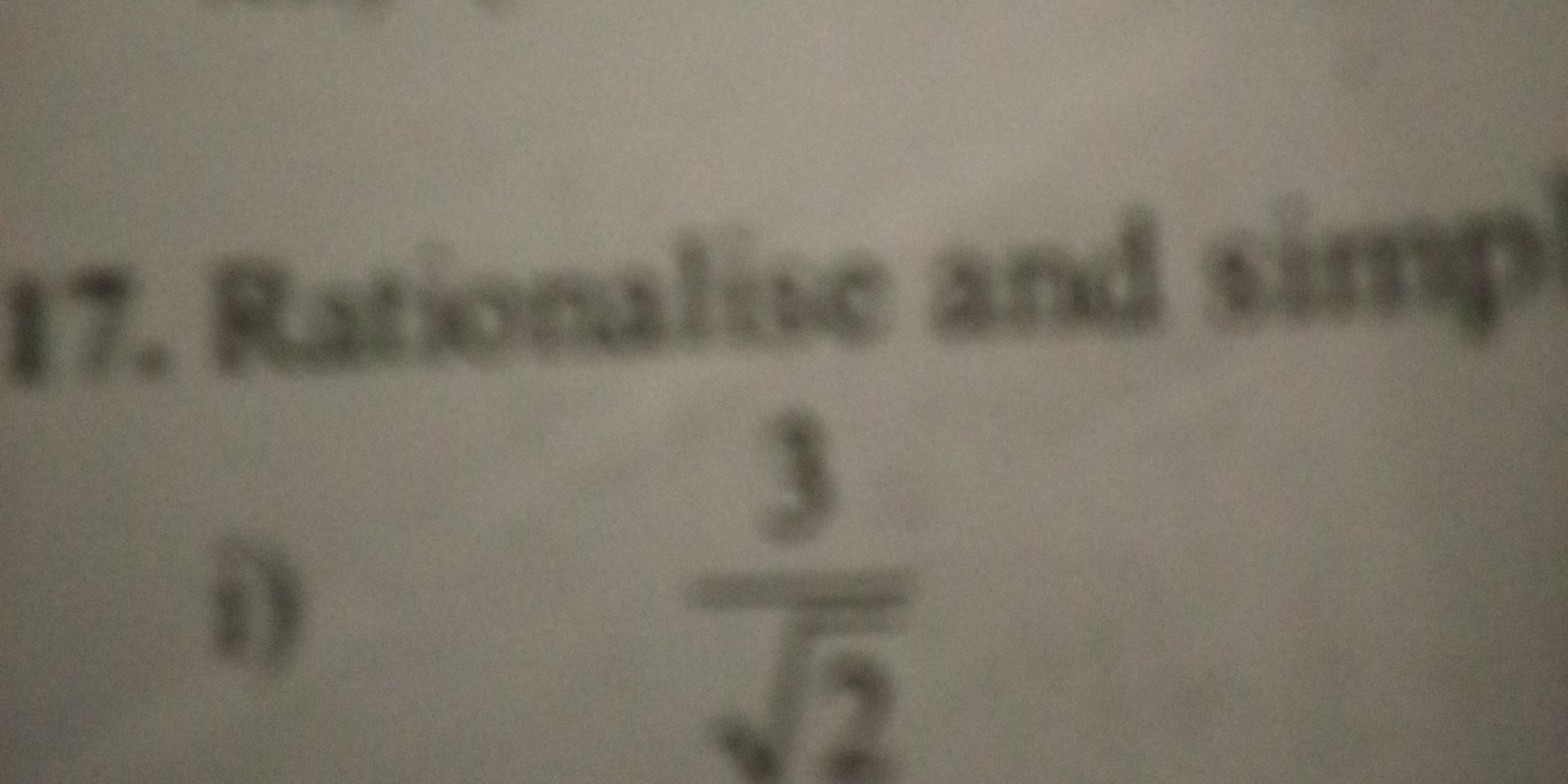
Understand the Problem
The question asks to rationalize the denominator of the fraction and simplify the expression. This involves multiplying both the numerator and the denominator by $\sqrt{2}$.
Answer
$\frac{3\sqrt{2}}{2}$
Answer for screen readers
$\frac{3\sqrt{2}}{2}$
Steps to Solve
- Identify the expression
The given expression is $\frac{3}{\sqrt{2}}$.
- Multiply the numerator and the denominator by $\sqrt{2}$
To rationalize the denominator, we multiply both the numerator and the denominator by $\sqrt{2}$. $$ \frac{3}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} $$
- Simplify the numerator
Multiplying the numerators gives: $$ 3 \cdot \sqrt{2} = 3\sqrt{2} $$
- Simplify the denominator
Multiplying the denominators gives: $$ \sqrt{2} \cdot \sqrt{2} = 2 $$
- Write the rationalized expression
Combining the simplified numerator and denominator, we get: $$ \frac{3\sqrt{2}}{2} $$
$\frac{3\sqrt{2}}{2}$
More Information
Rationalizing the denominator means rewriting a fraction so that there are no radical expressions in the denominator. This makes it easier to approximate the value of the expression and to compare different expressions.
Tips
A common mistake is only multiplying the denominator by $\sqrt{2}$, forgetting to also multiply the numerator. This changes the value of the expression. To avoid this, remember to multiply both the numerator and denominator by the same value, which is equivalent to multiplying the entire fraction by 1, thus preserving its value.
AI-generated content may contain errors. Please verify critical information