Simplify the expression: 1.5 * (3x^-3) / (3x)^2

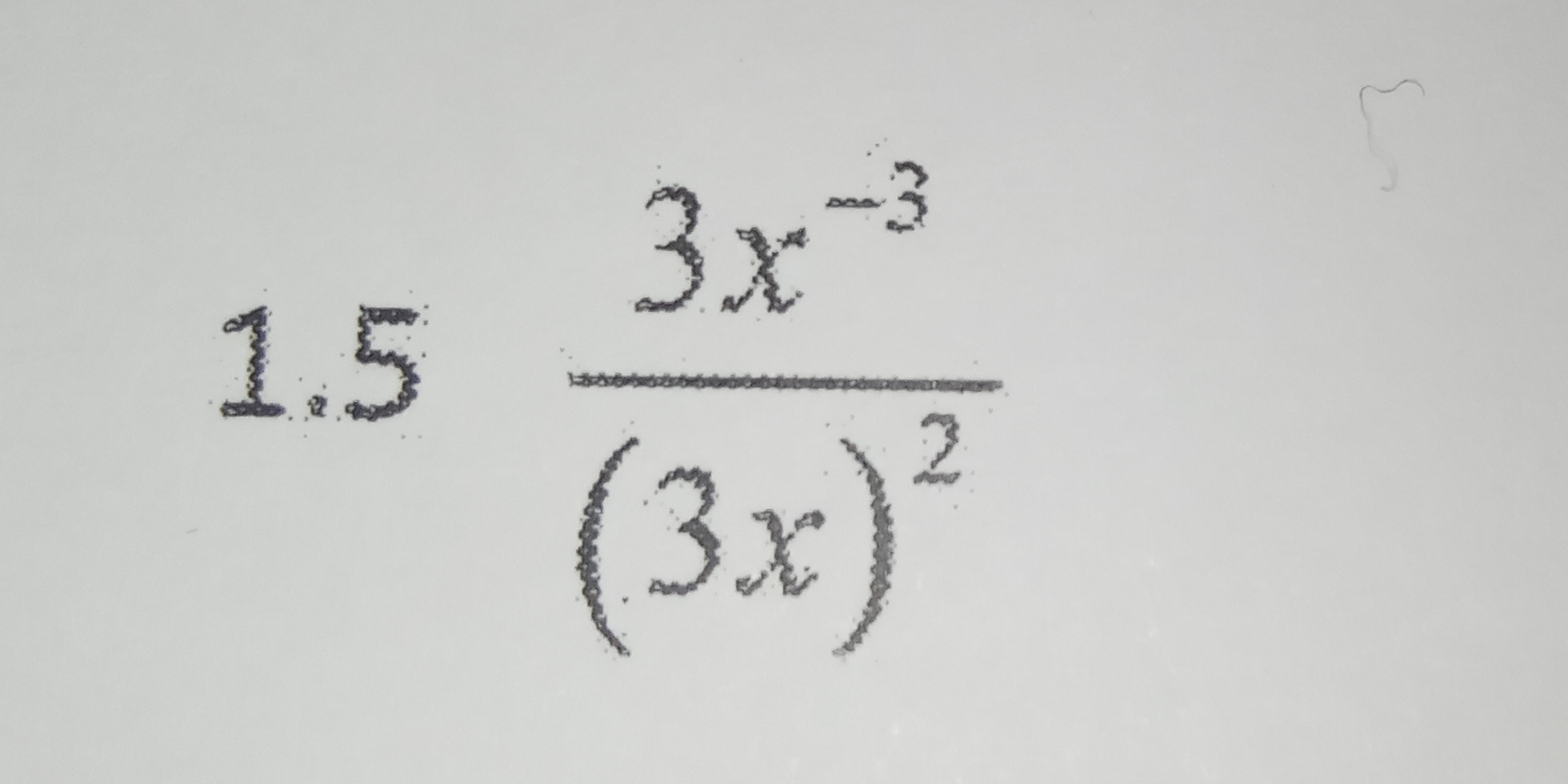
Understand the Problem

The question asks us to simplify the given expression involving exponents and fractions. We need to follow the order of operations, apply exponent rules, and then simplify the numerical factors.

Answer

$\frac{1}{2x^5}$

Steps to Solve

Expand the denominator Apply the power of a product rule to expand $(3x)^2$

$(3x)^2= 3^2 * x^2 = 9x^2$

Rewrite the expression Substitute the expanded denominator into the original expression:

$1.5 \frac{3x^{-3}}{9x^2}$

Simplify the fraction Divide the constants and apply the quotient rule for exponents: $\frac{x^a}{x^b} = x^{a-b}$

$\frac{3}{9} = \frac{1}{3}$

$\frac{x^{-3}}{x^2} = x^{-3-2} = x^{-5}$

So the expression becomes:

$1.5 * \frac{1}{3} * x^{-5}$

Rewrite 1.5 as a fraction

$1.5 = \frac{3}{2}$

Multiply the constants

$\frac{3}{2} * \frac{1}{3} = \frac{1}{2}$

Then we have:

$\frac{1}{2} * x^{-5}$

Rewrite with a positive exponent Use the rule $x^{-a} = \frac{1}{x^a}$

$\frac{1}{2} * x^{-5} = \frac{1}{2} * \frac{1}{x^5} = \frac{1}{2x^5}$

$\frac{1}{2x^5}$

More Information

The expression is simplified by expanding the denominator, applying the rules of exponents, and simplifying the resulting constants. Rewriting negative exponents as positive exponents leads to the final form of the simplified expression.

Tips

Forgetting to apply the exponent to both the coefficient and the variable when expanding $(3x)^2$.
Incorrectly applying the quotient rule of exponents when dividing terms with the same base.
Not simplifying the numerical coefficients correctly.
Forgetting to convert the final expression so that it only contains positive exponents.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!