If a patient's pulse measures 70, then 80, then 120, what least squares value minimizes (x - 70)² + (x - 80)² + (x - 120)²? If the patient got nervous, assign 120 a lower weight an... If a patient's pulse measures 70, then 80, then 120, what least squares value minimizes (x - 70)² + (x - 80)² + (x - 120)²? If the patient got nervous, assign 120 a lower weight and minimize (x - 70)² + (x - 80)² + k(x - 120)².
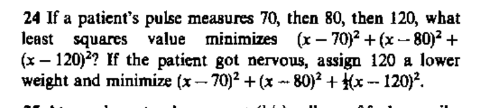
Understand the Problem
The question is asking to find the least squares value that minimizes the given expressions involving the pulse measurements. It also introduces a weighted approach due to the patient's nervousness, where the weight of 120 is reduced, highlighting the concepts of maxima and minima in optimization.
Answer
The unweighted least squares value is \(x = 90\). The weighted case yields \(x = \frac{300 + 240k}{2(1 + k)}\).
Answer for screen readers
The least squares value that minimizes the original expression is (x = 90). For the weighted case, the minimum occurs at: $$x = \frac{300 + 240k}{2(1 + k)}$$
Steps to Solve
- Set Up the Equation for Least Squares
To find the least squares value, we need to minimize the expression: $$(x - 70)^2 + (x - 80)^2 + (x - 120)^2$$
- Expand the Squares
Expand each square in the equation:
-
For $(x - 70)^2$, we have: $$(x - 70)^2 = x^2 - 140x + 4900$$
-
For $(x - 80)^2$, we have: $$(x - 80)^2 = x^2 - 160x + 6400$$
-
For $(x - 120)^2$, we have: $$(x - 120)^2 = x^2 - 240x + 14400$$
Combining these, we get: $$f(x) = (x^2 - 140x + 4900) + (x^2 - 160x + 6400) + (x^2 - 240x + 14400)$$
- Combine Like Terms
Now, combine the terms: $$f(x) = 3x^2 - 540x + (4900 + 6400 + 14400)$$ $$= 3x^2 - 540x + 27700$$
- Differentiate the Function
To find the minimum, we differentiate (f(x)) and set it to zero: $$f'(x) = 6x - 540$$ Now, set the derivative equal to zero: $$6x - 540 = 0$$
- Solve for x
Solving for (x): $$6x = 540$$ $$x = 90$$
- Consider the Weighted Approach
Now, if the patient is nervous, we need to minimize: $$(x - 70)^2 + (x - 80)^2 + k(x - 120)^2$$
Expanding this similarly gives: $$f_w(x) = (x - 70)^2 + (x - 80)^2 + k(x - 120)^2$$
Expanding and combining will give: $$f_w(x) = (x^2 - 140x + 4900) + (x^2 - 160x + 6400) + k(x^2 - 240x + 14400)$$ $$= (2 + k)x^2 - (300 + 240k)x + (4900 + 6400 + 14400k)$$
- Differentiate Weighted Function
Differentiate (f_w(x)): $$f_w'(x) = 2(1 + k)x - (300 + 240k)$$
- Solve for x in Weighted Case
Setting this equal to zero: $$2(1 + k)x - (300 + 240k) = 0$$ $$x = \frac{300 + 240k}{2(1 + k)}$$
The least squares value that minimizes the original expression is (x = 90). For the weighted case, the minimum occurs at: $$x = \frac{300 + 240k}{2(1 + k)}$$
More Information
The least squares method is a common approach to minimize the sum of the squares of the differences between observed and predicted values. Adjusting weights reflects the importance of certain measurements, allowing for more accurate modeling based on varying patient conditions.
Tips
- Forgetting to expand the squares correctly.
- Not combining like terms after expansion.
- Overlooking the differentiation step.
AI-generated content may contain errors. Please verify critical information