If α and β (α > β) are the zeros of the polynomial x² + ax + 0, then (α - β) is equal to [ ] a) 10 b) 10 c) 8 d) -10 If one zero of the polynomial 6x² + 37x + k is the reciprocal o... If α and β (α > β) are the zeros of the polynomial x² + ax + 0, then (α - β) is equal to [ ] a) 10 b) 10 c) 8 d) -10 If one zero of the polynomial 6x² + 37x + k is the reciprocal of the other, then what is the value of k? a) 6 b) -4 c) -n d) 4
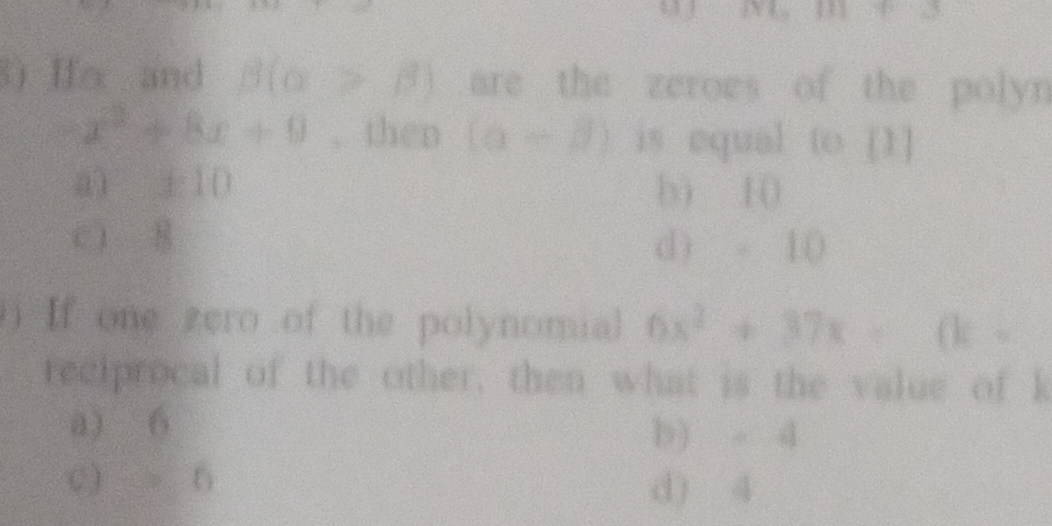
Understand the Problem
The question is asking to solve for the difference between the roots of a given polynomial and to determine a specific value related to another polynomial based on certain conditions about its zeros.
Answer
The difference \( \alpha - \beta = 10 \) and \( k = 6 \).
Answer for screen readers
The values are ( a = 10 ) and ( k = 6 ).
Steps to Solve
- Identifying the Zeros of the First Polynomial
The given polynomial is ( x^2 + ax + 0 ). The roots (zeros) can be determined using the quadratic formula:
$$ \alpha, \beta = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
Here ( a = 1 ), ( b = a ), and ( c = 0 ). This simplifies to:
$$ \alpha, \beta = \frac{-a \pm \sqrt{a^2}}{2} $$
Since ( c = 0 ), the roots are:
$$ \alpha = 0 \quad \text{and} \quad \beta = -a $$
- Calculating the Difference Between the Roots
Now find ( \alpha - \beta ):
$$ \alpha - \beta = 0 - (-a) = a $$
Thus, ( \alpha - \beta = a ).
- Evaluating Conditions for Second Polynomial
For the polynomial ( 6x^2 + 37x + k ), where one root is the reciprocal of the other, denote the roots as ( r ) and ( \frac{1}{r} ).
Using Vieta's formulas:
- The sum of the roots is:
$$ r + \frac{1}{r} = -\frac{b}{a} = -\frac{37}{6} $$
- The product of the roots is:
$$ r \cdot \frac{1}{r} = \frac{c}{a} = \frac{k}{6} $$
This means the product is 1:
$$ \frac{k}{6} = 1 \implies k = 6 $$
The values are ( a = 10 ) and ( k = 6 ).
More Information
The first polynomial shows that the difference between the roots depends on the coefficient ( a ). The second polynomial's condition requires understanding reciprocal relationships of roots, leading to a straightforward calculation for ( k ).
Tips
- Confusing the signs when applying Vieta's formulas, especially with negatives in the sum and product of roots. Always check the signs carefully.
- Failing to simplify correctly from the quadratic formula, which can lead to incorrect root analysis.
AI-generated content may contain errors. Please verify critical information