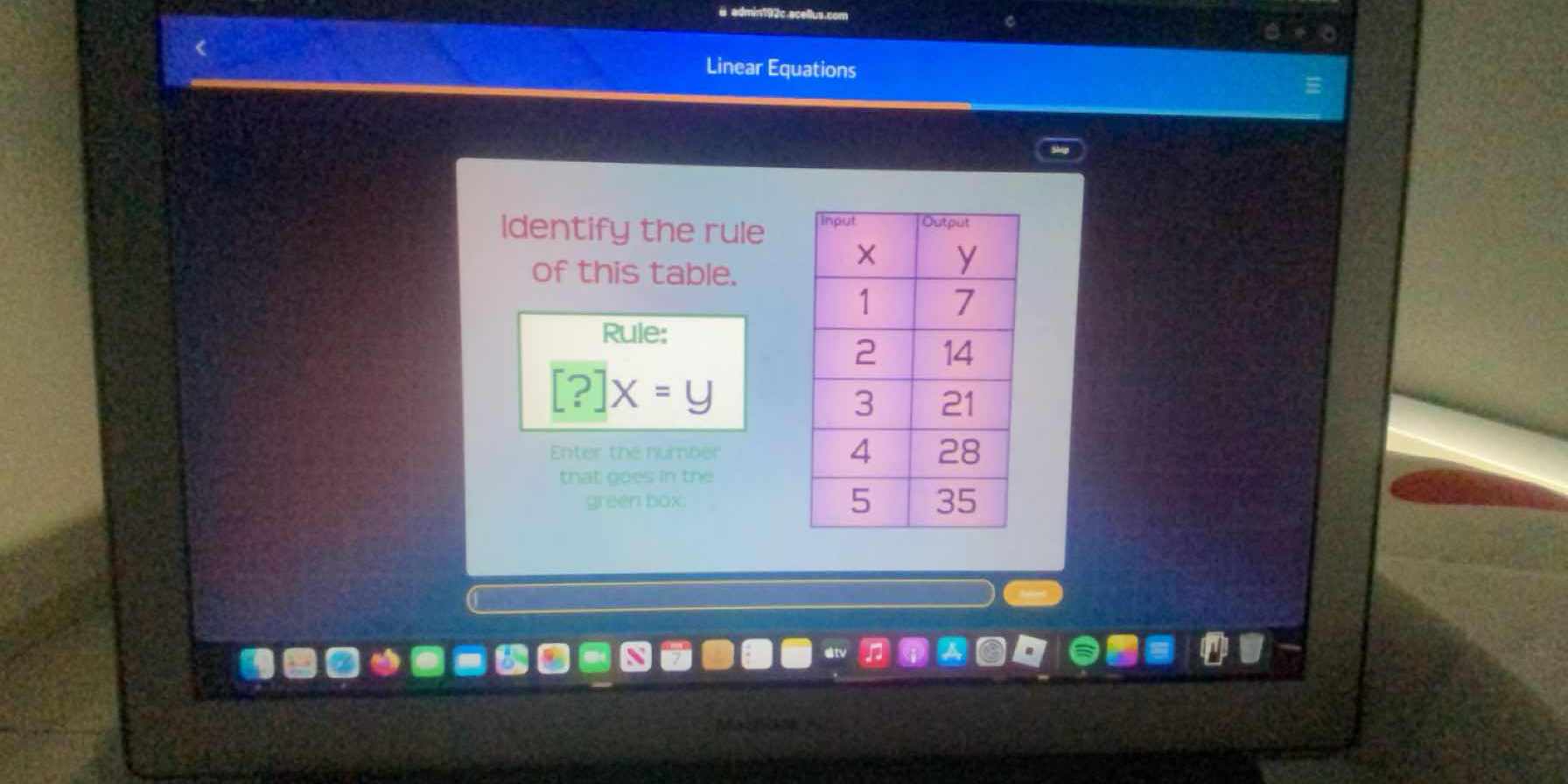
Identify the rule of this table.
Understand the Problem
The question is asking to identify the mathematical rule that relates the input values (x) to the output values (y) in the given table. The objective is to find the missing number that fits into the equation x = y.
Answer
The rule is $y = 7x$ and the missing number is $7$.
Answer for screen readers
Steps to Solve
- Identify Input and Output Values
From the table, we have the following pairs of input (x) and output (y):
- For $x = 1$, $y = 7$
- For $x = 2$, $y = 14$
- For $x = 3$, $y = 21$
- For $x = 4$, $y = 28$
- For $x = 5$, $y = 35$
- Find the Relationship
Let's see what happens when we multiply each $x$ by a certain number:
- $1 \cdot ? = 7$
- $2 \cdot ? = 14$
- $3 \cdot ? = 21$
- $4 \cdot ? = 28$
- $5 \cdot ? = 35$
Now, let's find the constant multiplier (?).
- Calculate the Multiplier
By examining the pairs:
- For $x = 1$: $? = 7$ (since $1 \cdot 7 = 7$)
- For $x = 2$: $? = 7$ (since $2 \cdot 7 = 14$)
- For $x = 3$: $? = 7$ (since $3 \cdot 7 = 21$)
- For $x = 4$: $? = 7$ (since $4 \cdot 7 = 28$)
- For $x = 5$: $? = 7$ (since $5 \cdot 7 = 35$)
So, the consistent multiplier we can use is $7$.
- Write the Rule
The rule relates the input x to the output y is:
$$ y = 7x $$
- Identify the Missing Number
Since the rule is $y = 7x$, to find the missing number in the green box:
When $x = ?$ it would be:
$$ ? \cdot 7 = y $$
For $y = 14$, we can find $?$:
$$ ? = \frac{14}{7} = 2 $$
More Information
This problem illustrates a linear relationship where the output is always a multiple of the input. The multiplier, here 7, indicates how much the output increases relative to the input.
Tips
- Confusing the inputs and outputs; always double-check which numbers correspond to x and y.
- Miscalculating simple multiplication; practice basic multiplication to avoid mistakes.
AI-generated content may contain errors. Please verify critical information