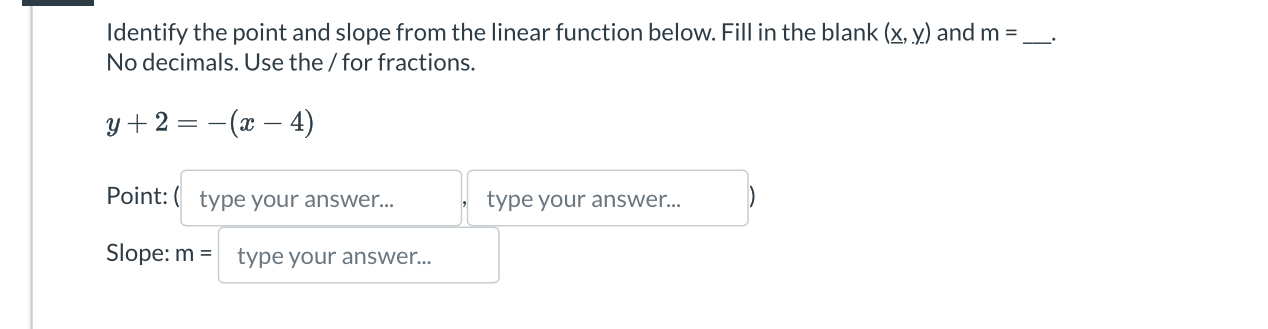
Identify the point and slope from the linear function below. Fill in the blank (x, y) and m = __. y + 2 = -(x - 4)
Understand the Problem
The question asks to identify the point and slope from the given linear function. We will need to rewrite the equation in slope-intercept form (y = mx + b) to find the slope and a point on the line.
Answer
Point: \( (0, 2) \), Slope: \( m = -1 \)
Answer for screen readers
Point: ( (0, 2) )
Slope: ( m = -1 )
Steps to Solve
- Rewrite the equation in slope-intercept form
We start with the equation:
$$ y + 2 = -(x - 4) $$
To rewrite it, we first simplify the right side:
$$ y + 2 = -x + 4 $$
Now, isolate ( y ):
$$ y = -x + 4 - 2 $$
$$ y = -x + 2 $$
This is in the slope-intercept form ( y = mx + b ) where ( m ) is the slope and ( b ) is the y-intercept.
- Identify the slope
From the equation ( y = -x + 2 ), we see that the slope ( m ) is the coefficient of ( x ):
$$ m = -1 $$
- Find a point on the line
To find a point, we can now substitute ( x = 0 ) into the equation to find ( y ):
$$ y = -0 + 2 $$
$$ y = 2 $$
Thus, one point on the line is ( (0, 2) ).
Point: ( (0, 2) )
Slope: ( m = -1 )
More Information
The slope indicates that for every 1 unit increase in ( x ), ( y ) decreases by 1 unit. The point ( (0, 2) ) represents where the line crosses the y-axis.
Tips
- A common mistake is to misinterpret the equation when distributing negative signs. Ensure to simplify carefully.
- Forgetting to isolate ( y ) properly can lead to incorrect interpretation of the slope and point.
AI-generated content may contain errors. Please verify critical information