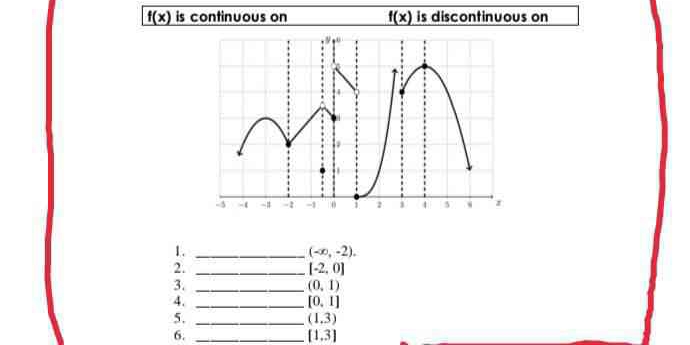
Identify the intervals where f(x) is continuous and discontinuous based on the graph provided.
Understand the Problem
The question asks to identify the intervals over which the function f(x) is continuous and discontinuous based on the provided graph. The user needs to analyze the graph to make these determinations.
Answer
- Continuous on: $(-\infty, -2), [-2, 0), (0, 1), (1, 3)$ - Discontinuous on: $(-2, 0), [1, 3)$
Answer for screen readers
- Continuous on:
- $(-\infty, -2)$
- $[-2, 0)$
- $(0, 1)$
- $(1, 3)$
- Discontinuous on:
- $(-2, 0)$
- $[1, 3) \cup (3, \infty)$
Steps to Solve
- Analyze the continuous sections of the graph
Look for intervals where the graph does not break or have any holes or vertical asymptotes. Based on the graph, the function appears to be continuous in the following intervals:
- $(-\infty, -2)$
- $[-2, 0)$
- $(0, 1)$
- $(1, 3)$
- Identify the discontinuous sections of the graph
Next, identify any points where the graph is not continuous, which are often indicated by breaks, holes, or vertical asymptotes. The function is discontinuous in the following intervals:
- $(-2, 0)$
- $[1, 3)$
- Fill in the intervals based on the graph analysis
With the gathered information, we can now place the intervals into the provided table slots indicating continuity and discontinuity.
- Continuous on:
- $(-\infty, -2)$
- $[-2, 0)$
- $(0, 1)$
- $(1, 3)$
- Discontinuous on:
- $(-2, 0)$
- $[1, 3) \cup (3, \infty)$
More Information
In general, a function is continuous at a point if it does not have any interruptions in its values at and around that point. Discontinuities can occur due to vertical asymptotes, removable discontinuities (holes), or step-like discontinuities.
Tips
- Misidentifying discontinuities: Be sure to check for vertical asymptotes or holes in the graph carefully.
- Overlooking endpoints: Make sure to consider whether endpoints are included (closed intervals) or not (open intervals).
AI-generated content may contain errors. Please verify critical information