How many integral solutions are there to x1 + x2 + x3 + x4 + x5 + x6 = 20, where x1 ≥ 3, x2 ≥ 2, x3 ≥ 2, x4 ≥ 2, x5 ≥ 1, x6 ≥ 0?
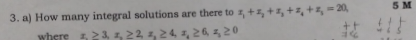
Understand the Problem
The question is asking for the number of integral solutions to an equation involving six variables that sum up to 20, with specified constraints on the minimum values of each variable.
Answer
The number of integral solutions is \( 792 \).
Answer for screen readers
The number of integral solutions is ( 792 ).
Steps to Solve
- Define the variables with minimum values
We have the equation ( z_1 + z_2 + z_3 + z_4 + z_5 + z_6 = 20 ) with constraints:
- ( z_1 \geq 3 )
- ( z_2 \geq 2 )
- ( z_3 \geq 2 )
- ( z_4 \geq 4 )
- ( z_5 \geq 2 )
- ( z_6 \geq 0 )
- Adjust for the minimum values
To simplify the problem, we will redefine the variables:
- Let ( z_1' = z_1 - 3 ) (hence ( z_1' \geq 0 ))
- Let ( z_2' = z_2 - 2 ) (hence ( z_2' \geq 0 ))
- Let ( z_3' = z_3 - 2 ) (hence ( z_3' \geq 0 ))
- Let ( z_4' = z_4 - 4 ) (hence ( z_4' \geq 0 ))
- Let ( z_5' = z_5 - 2 ) (hence ( z_5' \geq 0 ))
- ( z_6' = z_6 ) (hence ( z_6' \geq 0 ))
Now, we can substitute these back into the equation:
$$ z_1' + z_2' + z_3' + z_4' + z_5' + z_6' + 3 + 2 + 2 + 4 + 2 + 0 = 20 $$
Thus, we simplify it to:
$$ z_1' + z_2' + z_3' + z_4' + z_5' + z_6' = 20 - (3 + 2 + 2 + 4 + 2) $$
- Calculate the new equation
Calculating the right-hand side gives:
$$ 20 - 13 = 7 $$
So we have:
$$ z_1' + z_2' + z_3' + z_4' + z_5' + z_6' = 7 $$
- Apply the stars and bars method
The number of non-negative integer solutions to the equation
$$ x_1 + x_2 + ... + x_k = n $$
is given by the formula:
$$ \binom{n + k - 1}{k - 1} $$
where ( n ) is the total and ( k ) is the number of variables.
In our case, ( n = 7 ) and ( k = 6 ):
- Substitute into the formula
Now, we can find the number of solutions:
$$ \binom{7 + 6 - 1}{6 - 1} = \binom{12}{5} $$
- Calculate the binomial coefficient
Finally, calculate ( \binom{12}{5} ):
$$ \binom{12}{5} = \frac{12 \times 11 \times 10 \times 9 \times 8}{5 \times 4 \times 3 \times 2 \times 1} = 792 $$
The number of integral solutions is ( 792 ).
More Information
This problem uses combinatorial methods, specifically the stars and bars theorem, to count the number of ways to partition a total among several variables given specific constraints.
Tips
- Forgetting to adjust for the minimum values of each variable before using the stars and bars method.
- Miscounting the number of variables or the total value after adjustments.
AI-generated content may contain errors. Please verify critical information