How many distinct solutions does the equation log10 x = 2 - log10 (x - 21) have?
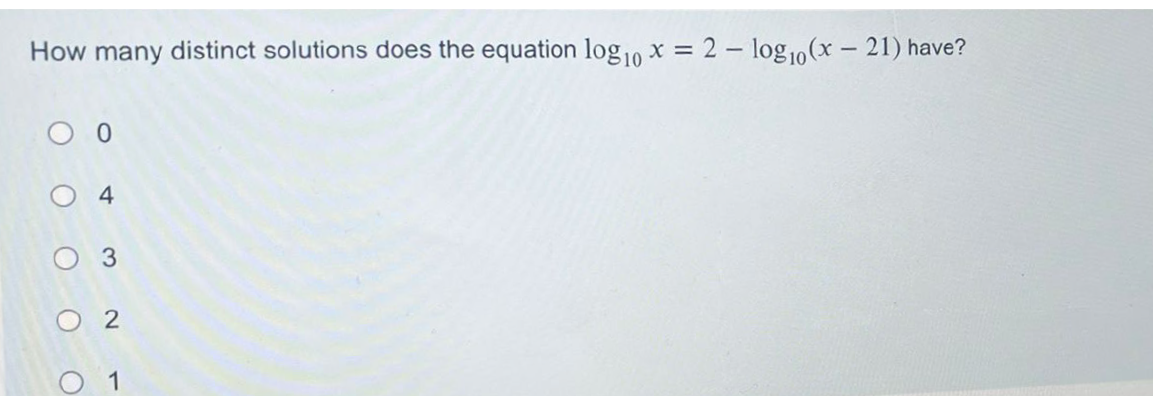
Understand the Problem
The question is asking to determine the number of distinct solutions for the logarithmic equation given. We'll analyze the equation step-by-step to derive the solutions.
Answer
1 distinct solution: $x = 25$
Answer for screen readers
The equation has 1 distinct solution: $x = 25$.
Steps to Solve
-
Rewrite the logarithmic equation We start with the given equation: $$ \log_{10} x = 2 - \log_{10} (x - 21) $$
-
Combine the logarithms To simplify, we can rewrite the equation by moving the logarithmic term: $$ \log_{10} x + \log_{10} (x - 21) = 2 $$
Using the property of logarithms that states $\log_b a + \log_b c = \log_b(ac)$, we combine: $$ \log_{10} [x(x - 21)] = 2 $$
-
Exponentiate to remove the logarithm Next, we exponentiate both sides to eliminate the logarithm: $$ x(x - 21) = 10^2 $$ This simplifies to: $$ x^2 - 21x - 100 = 0 $$
-
Solve the quadratic equation We will use the quadratic formula, where $a = 1$, $b = -21$, and $c = -100$: $$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$ Calculating the discriminant: $$ b^2 - 4ac = (-21)^2 - 4(1)(-100) = 441 + 400 = 841 $$
The square root of 841 is 29.
- Find the values of x Plugging the values back into the formula: $$ x = \frac{21 \pm 29}{2} $$
Calculating the two possible values:
-
( x_1 = \frac{50}{2} = 25 )
-
( x_2 = \frac{-8}{2} = -4 )
-
Check valid solutions The logarithm $\log_{10} (x - 21)$ requires ( x - 21 > 0 ), which implies ( x > 21 ). Thus, only take ( x_1 = 25 ) as a valid solution.
The equation has 1 distinct solution: $x = 25$.
More Information
In logarithmic equations, it's crucial to ensure that all arguments of the logarithms are valid (i.e., positive) when solving the equations.
Tips
- Ignoring valid ranges of variables: Always check the domain of the variables involved in logarithmic equations to avoid invalid solutions.
- Miscalculating the discriminant: Ensure correct arithmetic operations when finding the discriminant; it's essential for determining the nature of the solutions.
AI-generated content may contain errors. Please verify critical information