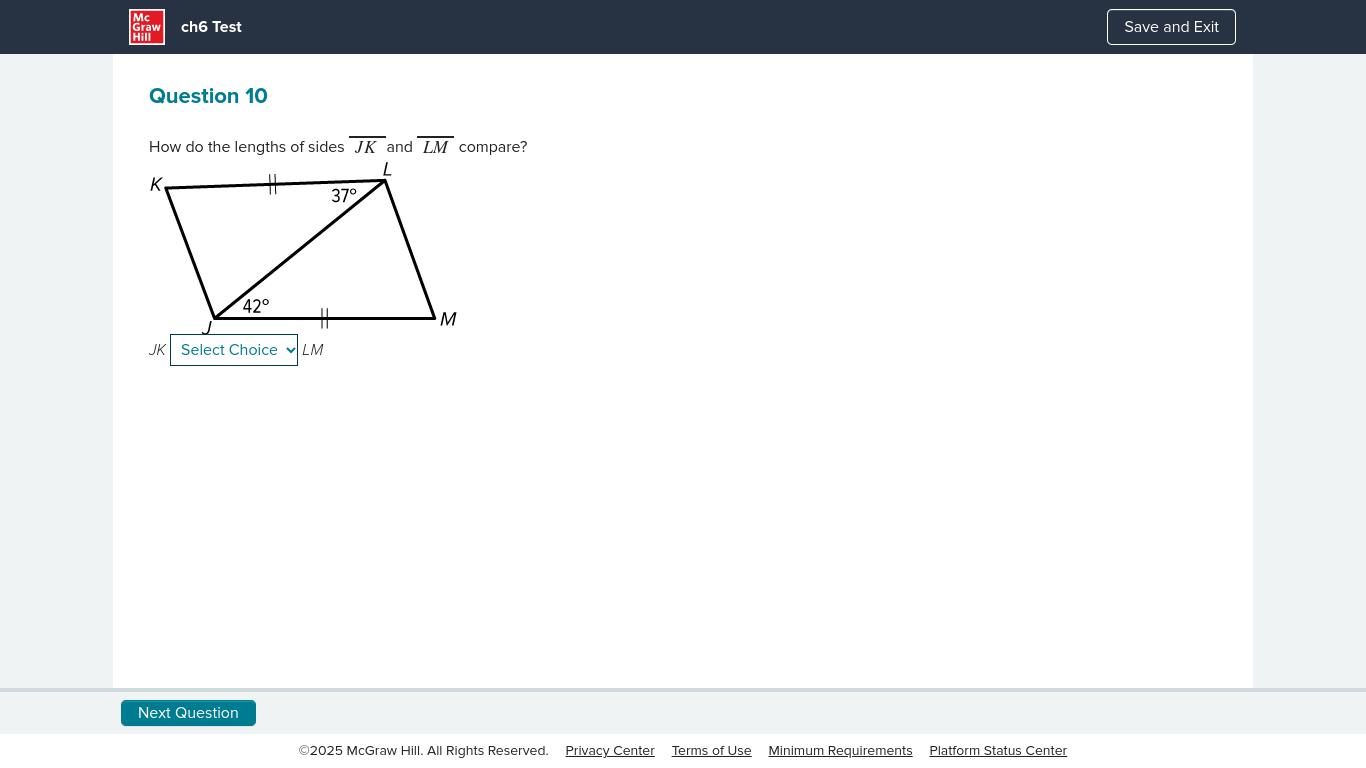
How do the lengths of sides JK and LM compare?

Steps to Solve

1. Identify the geometric shape and given angles The provided diagram shows a quadrilateral with angles indicated. We have angles ( \angle KJL = 42^\circ ) and ( \angle LJM = 37^\circ ).

2. Apply properties of angles in a quadrilateral In any quadrilateral, the sum of the interior angles is ( 360^\circ ). We can express this relationship with the formula: $$ \angle KJL + \angle LJM + \angle MLK + \angle KLM = 360^\circ $$

3. Calculate the third angle ( \angle MLK ) Since both angles ( \angle KJL ) and ( \angle LJM ) are known: $$ \angle MLK = 360^\circ - (42^\circ + 37^\circ) = 360^\circ - 79^\circ = 281^\circ $$

4. Determine the relationship between sides JK and LM The angles ( \angle KJL ) and ( \angle LJM ) can help establish that they relate to the lengths of the opposite sides ( JK ) and ( LM ) respectively. According to the properties of triangles, if (\angle KJL < \angle LJM), then the side opposite to the larger angle (here, (LM)) is longer.

5. Conclude the side comparison Since ( \angle KJL = 42^\circ ) is less than ( \angle LJM = 37^\circ ), we can conclude: $$ JK < LM $$