Horizontal velocity will be?
Understand the Problem
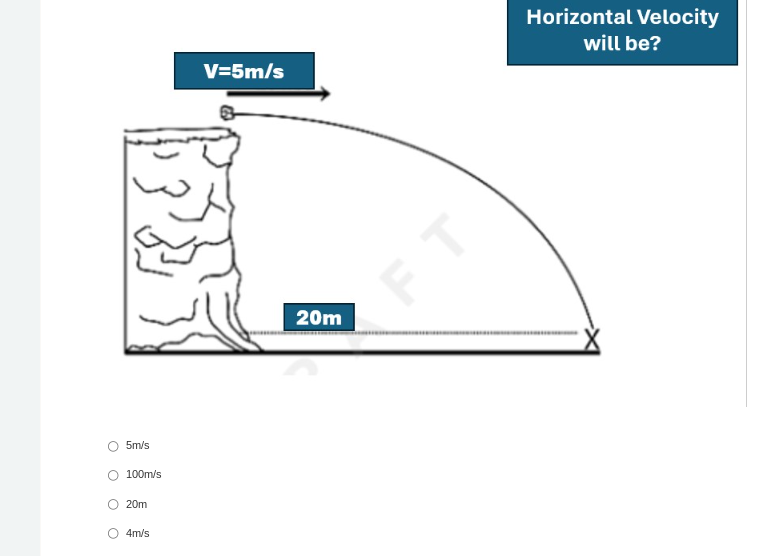
The question is asking for the horizontal velocity of an object that is projected at a certain speed (5 m/s) horizontally from a height of 20 m. The problem likely requires the use of kinematic equations to analyze the motion of the object.
Answer
The horizontal velocity will be $5 \, m/s$.
Answer for screen readers
The horizontal velocity will be $5 , m/s$.
Steps to Solve
- Identify the Given Information
The object is projected horizontally with a speed of $V = 5 , m/s$ from a height of $h = 20 , m$.
- Determine the Time of Flight
We need to find the time it takes for the object to fall 20 meters. Using the equation for falling objects under gravity:
$$ h = \frac{1}{2} g t^2 $$
where $g = 9.81 , m/s^2$ is the acceleration due to gravity. Rearranging this gives:
$$ t = \sqrt{\frac{2h}{g}} $$
- Calculate the Time of Flight
Substituting the values:
$$ t = \sqrt{\frac{2 \cdot 20}{9.81}} $$
Calculating this value:
$$ t \approx \sqrt{\frac{40}{9.81}} \approx \sqrt{4.08} \approx 2.02 , s $$
- Find the Horizontal Distance
The horizontal velocity is constant, so we use the time of flight to determine how far the object travels horizontally:
$$ d = V \cdot t $$
Substituting the values:
$$ d = 5 , m/s \cdot 2.02 , s \approx 10.1 , m $$
- Result Interpretation
The horizontal velocity remains $5 , m/s$, as it is not affected by vertical motion.
The horizontal velocity will be $5 , m/s$.
More Information
In projectile motion, the horizontal component of velocity remains constant, while the vertical component is influenced by gravity. This ensures the object's horizontal speed stays at $5 , m/s$, regardless of the height from which it is projected.
Tips
There are no common mistakes specific to this problem.
AI-generated content may contain errors. Please verify critical information