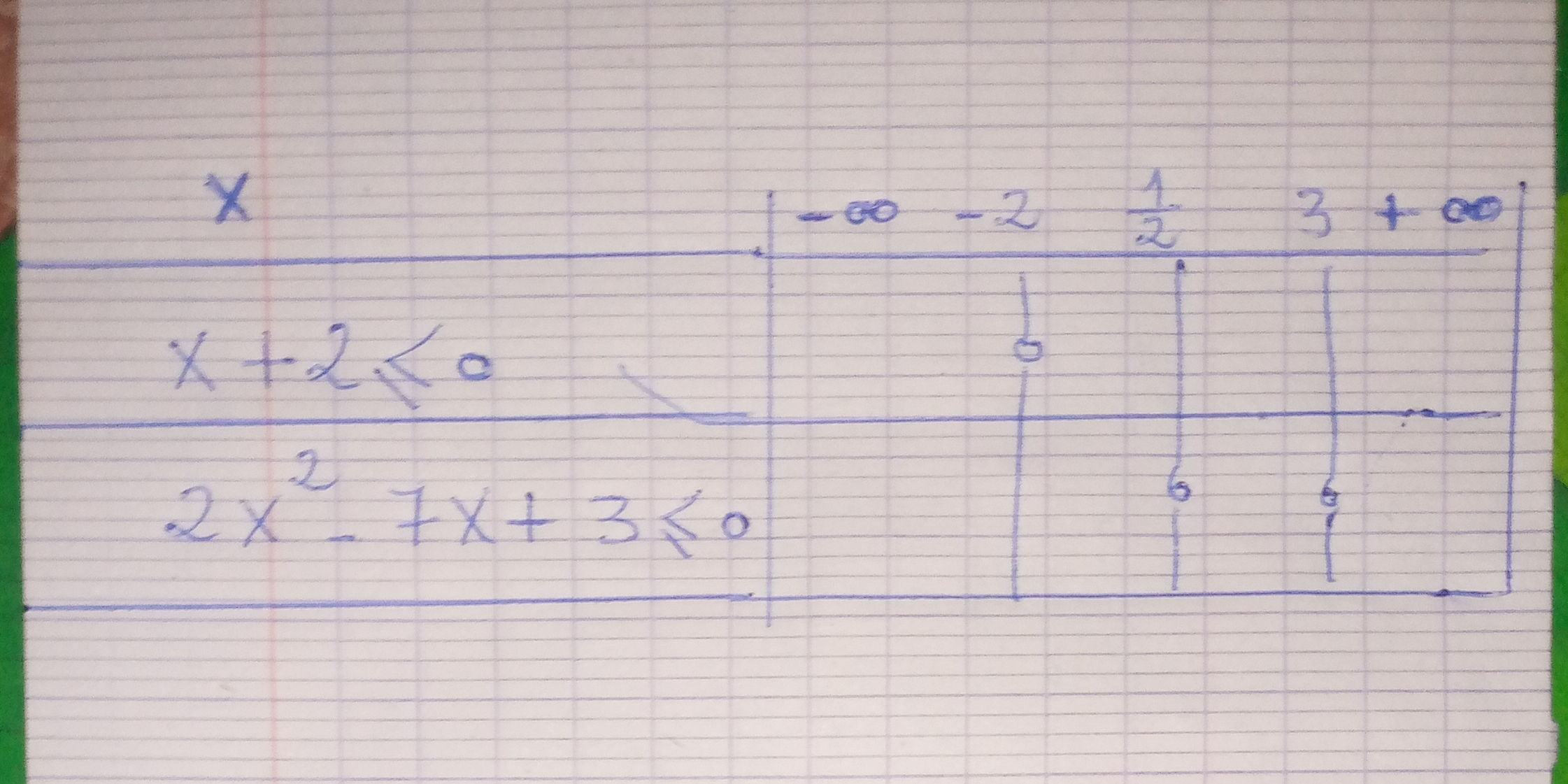
Graph the inequalities x + 2 < 0 and 2x^2 - 7x + 3 < 0.

Steps to Solve

1. Solve the First Inequality

   The first inequality is given as ( x + 2 < 0 ).

   To solve for ( x ), subtract 2 from both sides: $$ x < -2 $$

2. Solve the Second Inequality

   The second inequality is ( 2x^2 - 7x + 3 < 0 ).

   First, we need to find the roots of the quadratic equation ( 2x^2 - 7x + 3 = 0 ). We can use the quadratic formula: $$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$ Here, ( a = 2 ), ( b = -7 ), and ( c = 3 ).

   Calculate the discriminant: $$ b^2 - 4ac = (-7)^2 - 4(2)(3) = 49 - 24 = 25 $$

   Now plug values into the formula to find the roots: $$ x = \frac{7 \pm \sqrt{25}}{2 \cdot 2} = \frac{7 \pm 5}{4} $$

   Calculate the roots: $$ x_1 = \frac{12}{4} = 3 $$ $$ x_2 = \frac{2}{4} = \frac{1}{2} $$

   The roots are ( x = 3 ) and ( x = \frac{1}{2} ).

3. Test Intervals for the Quadratic Inequality

   We will test intervals around the roots ( x = \frac{1}{2} ) and ( x = 3 ). The intervals are:

   • ( (-\infty, \frac{1}{2}) )
   • ( \left(\frac{1}{2}, 3\right) )
   • ( (3, +\infty) )

   Choose test points:

   • For ( x = 0 ) in ( (-\infty, \frac{1}{2}) ): $$ 2(0)^2 - 7(0) + 3 = 3 > 0 $$
   • For ( x = 2 ) in ( \left(\frac{1}{2}, 3\right) ): $$ 2(2)^2 - 7(2) + 3 = 8 - 14 + 3 = -3 < 0 $$
   • For ( x = 4 ) in ( (3, +\infty) ): $$ 2(4)^2 - 7(4) + 3 = 32 - 28 + 3 = 7 > 0 $$

   Thus, the inequality ( 2x^2 - 7x + 3 < 0 ) is satisfied in the interval ( \left(\frac{1}{2}, 3\right) ).

4. Combine the Results

   Combine the results from both inequalities:

   • From ( x + 2 < 0 ): ( x < -2 )
   • From ( 2x^2 - 7x + 3 < 0 ): ( \frac{1}{2} < x < 3 )

   The two inequalities do not overlap, so we have two separate solutions.