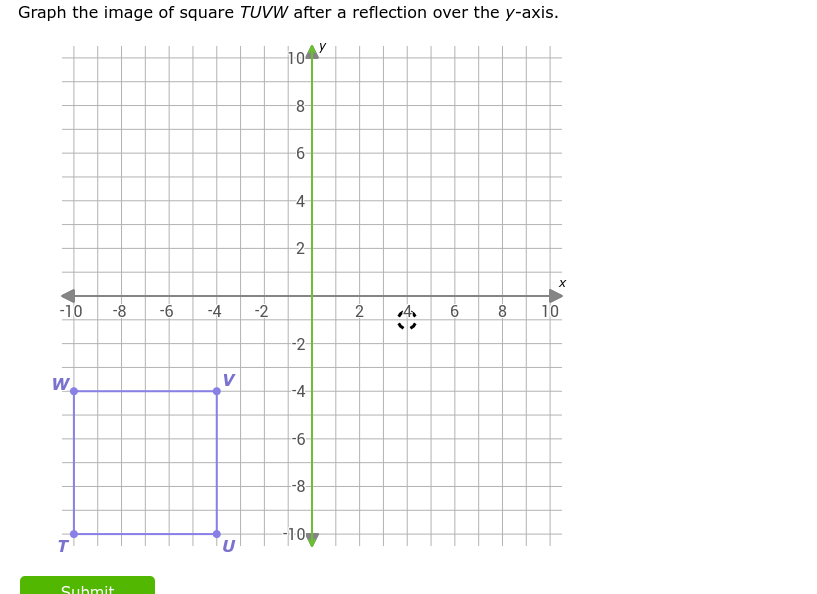
Graph the image of square TUVW after a reflection over the y-axis.

Understand the Problem

The question is asking for the graph of a square after it has been reflected over the y-axis. This involves determining the new coordinates of the vertices of the square based on the reflection rule for points across the y-axis.

Answer

The reflected square has vertices $T'(4, -4)$, $U'(4, -6)$, $V'(2, -4)$, and $W'(2, -6)$.

Steps to Solve

Identify the coordinates of the original square vertices

Let's assume the square $TUVW$ has the following coordinates:

$T(-4, -4)$
$U(-4, -6)$
$V(-2, -4)$
$W(-2, -6)$

Apply the reflection rule over the y-axis

In reflection across the y-axis, the x-coordinate changes sign while the y-coordinate remains the same.

For our vertices, the new coordinates will be:

$T'$ will be $(4, -4)$
$U'$ will be $(4, -6)$
$V'$ will be $(2, -4)$
$W'$ will be $(2, -6)$

Plot the new vertices on the graph

Plot the new coordinates:

$T'(4, -4)$
$U'(4, -6)$
$V'(2, -4)$
$W'(2, -6)$

Draw the square

Connect the points $T'$, $U'$, $V'$, and $W'$ to complete the graph of the reflected square.

The coordinates of the reflected square $T'U'V'W'$ are:

$T'(4, -4)$
$U'(4, -6)$
$V'(2, -4)$
$W'(2, -6)$

More Information

Reflecting a figure over the y-axis allows us to visualize symmetry. The resulting shape maintains the same dimensions and orientation but is positioned symmetrically relative to the y-axis.

Tips

null

AI-generated content may contain errors. Please verify critical information

Thank you for voting!