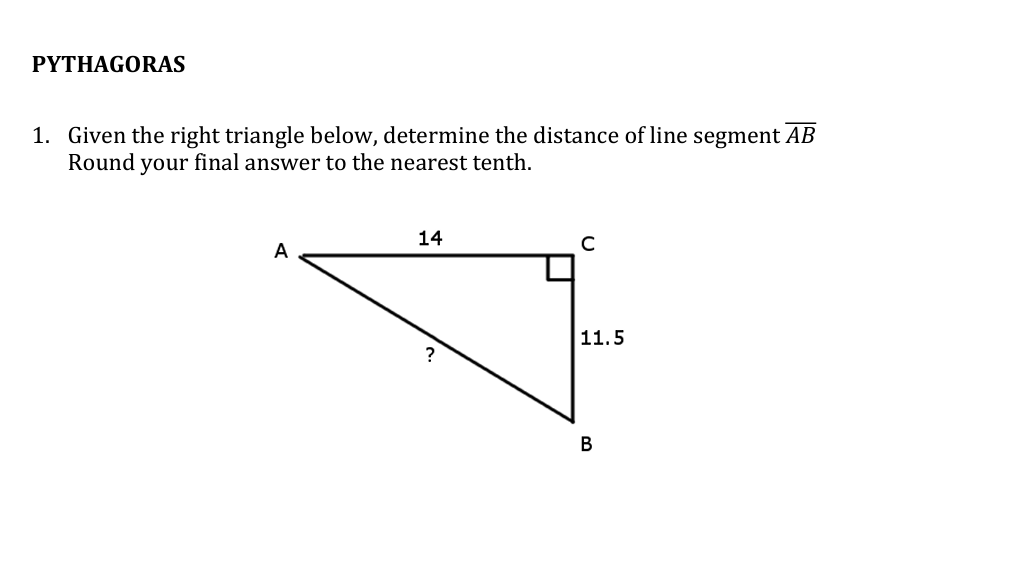
Given the right triangle below, determine the distance of line segment AB. Round your final answer to the nearest tenth.
Understand the Problem
The question is asking us to calculate the length of line segment AB in a right triangle using the Pythagorean theorem. We know two sides of the triangle: AC is 14 units and BC is 11.5 units. We need to find the length of AB and round the final answer to the nearest tenth.
Answer
$18.1$
Answer for screen readers
The length of line segment ( AB ) is approximately $18.1$ units.
Steps to Solve
- Identify the sides of the triangle
In the right triangle ( ABC ), we know that:
- ( AC = 14 ) units (one leg),
- ( BC = 11.5 ) units (the other leg),
- ( AB ) is the hypotenuse (the side we want to find).
- Apply the Pythagorean theorem
The Pythagorean theorem states that in a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. We can express this as:
$$ AB^2 = AC^2 + BC^2 $$
- Substitute the known values into the equation
Replace ( AC ) and ( BC ) with their respective lengths:
$$ AB^2 = 14^2 + 11.5^2 $$
Calculating the squares:
$$ AB^2 = 196 + 132.25 $$
- Simplify and calculate ( AB^2 )
Now, add the two results:
$$ AB^2 = 196 + 132.25 = 328.25 $$
- Calculate ( AB ) by taking the square root
Now, to find ( AB ), we take the square root:
$$ AB = \sqrt{328.25} $$
Using a calculator gives:
$$ AB \approx 18.1 $$ (rounded to the nearest tenth)
The length of line segment ( AB ) is approximately $18.1$ units.
More Information
The Pythagorean theorem is a fundamental principle used in various fields, including physics, engineering, and architecture. The theorem can help determine distances and measurements when dealing with right triangles.
Tips
- Forgetting to square both legs before adding them together.
- Not using the square root to find the length of the hypotenuse.
- Rounding off too early in the calculations instead of at the final step.
