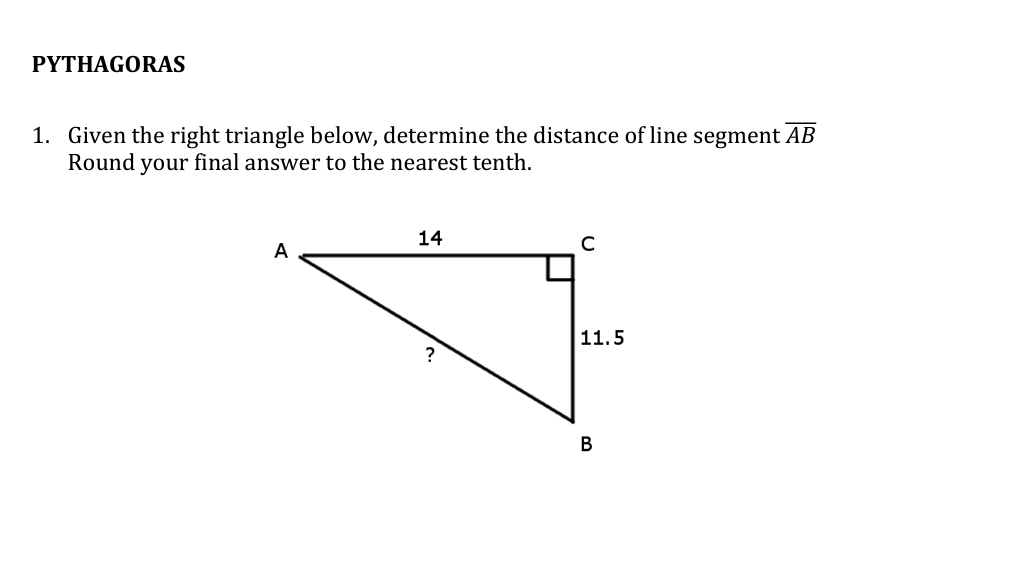
Given the right triangle below, determine the distance of line segment AB. Round your final answer to the nearest tenth.
Understand the Problem
The question is asking to find the length of line segment AB in a right triangle, using the provided lengths of sides AC and BC. This can be solved using the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Answer
The length of line segment $AB$ is approximately $8.0$.
Answer for screen readers
The length of line segment $AB$ is approximately $8.0$.
Steps to Solve
- Identify the sides of the triangle
Let $AB$ be the side we need to find, and identify the lengths given:
- Side $AC = 14$ (adjacent side)
- Side $BC = 11.5$ (opposite side)
- Apply the Pythagorean theorem
According to the Pythagorean theorem:
$$ AC^2 = AB^2 + BC^2 $$
We can rearrange this to find $AB$:
$$ AB^2 = AC^2 - BC^2 $$
- Substitute the known values
Now substitute the values we know into the equation:
$$ AB^2 = 14^2 - 11.5^2 $$
Calculating each square:
$$ AB^2 = 196 - 132.25 $$
- Calculate $AB^2$
Perform the subtraction:
$$ AB^2 = 63.75 $$
- Find $AB$ by taking the square root
Now take the square root to find $AB$:
$$ AB = \sqrt{63.75} $$
Calculating the square root gives approximately:
$$ AB \approx 7.99 $$
- Round to the nearest tenth
Round $7.99$ to the nearest tenth:
$$ AB \approx 8.0 $$
The length of line segment $AB$ is approximately $8.0$.
More Information
The Pythagorean theorem is a fundamental principle in geometry that applies to right triangles, making it useful for various calculations in mathematics, engineering, and physics. The hypotenuse is always the longest side opposite the right angle, and the theorem connects the square of its length to the squares of the lengths of the other two sides.
Tips
- Forgetting to square the sides: Always remember to square each side when applying the formula.
- Miscalculating the operations: Double-check arithmetic operations to avoid simple calculation errors.
- Neglecting to round: Ensure to round to the correct decimal place as required by the problem.