Given the right triangle below, determine the distance of line segment AB. Round your final answer to the nearest tenth.
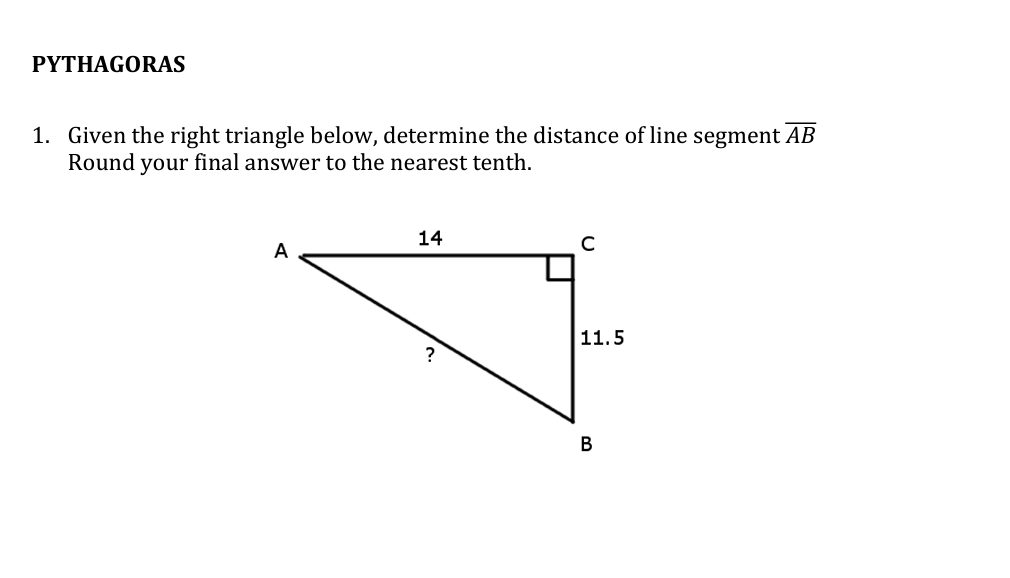
Understand the Problem
The question is asking to calculate the length of line segment AB in a right triangle using the Pythagorean theorem, given the lengths of the other two sides (14 and 11.5). We will apply the theorem: a² + b² = c², where c is the hypotenuse and a and b are the other two sides.
Answer
The length of line segment \(AB\) is approximately \(18.1\).
Answer for screen readers
The length of line segment (AB) is approximately (18.1).
Steps to Solve
- Identify the sides of the triangle
In the right triangle, we know the lengths of two sides: $AC = 14$ and $BC = 11.5$. We need to find the length of the line segment $AB$.
- Apply the Pythagorean theorem
According to the Pythagorean theorem, we can express the relationship between the sides as:
$$ AB^2 = AC^2 + BC^2 $$
- Substitute the known values
Plug in the known lengths into the equation:
$$ AB^2 = 14^2 + 11.5^2 $$
Calculating each term gives:
$$ AB^2 = 196 + 132.25 $$
- Calculate the sum and solve for (AB)
Add the values on the right side:
$$ AB^2 = 328.25 $$
Next, take the square root of both sides to find (AB):
$$ AB = \sqrt{328.25} $$
- Find the final answer and round
Calculating the square root gives:
$$ AB \approx 18.1 $$
Rounding to the nearest tenth, we have:
$$ AB \approx 18.1 $$
The length of line segment (AB) is approximately (18.1).
More Information
The Pythagorean theorem is fundamental in geometry, especially in relation to right triangles. This theorem allows us to find the relationship between the lengths of the sides, making it applicable in various real-life situations, such as architecture and construction.
Tips
- Forgetting to square the lengths before adding them.
- Confusing which side is the hypotenuse.
- Not rounding correctly to the nearest tenth.
AI-generated content may contain errors. Please verify critical information