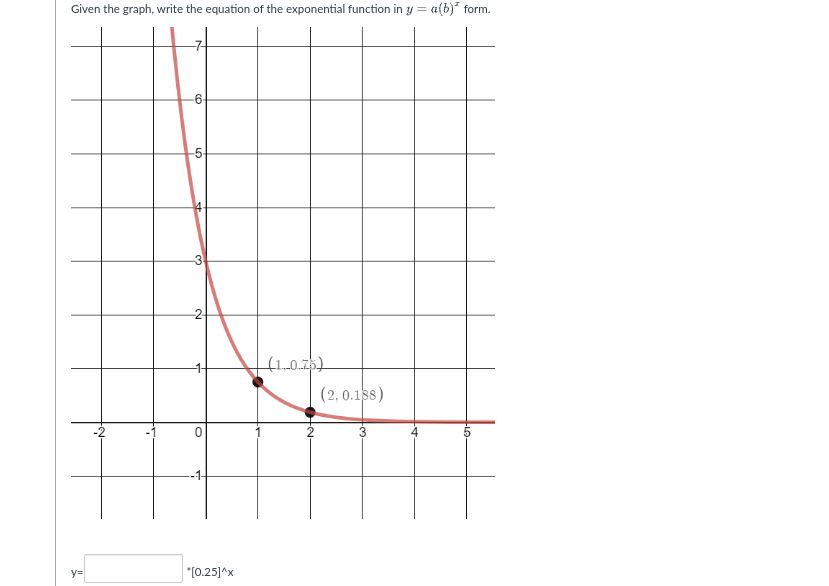
Given the graph, write the equation of the exponential function in y = a(b)^x form.

Steps to Solve

1. Identify Points on the Graph

From the graph, we have key points:

• Point 1: $(1, 0.75)$
• Point 2: $(2, 0.188)$

These points will help us solve for parameters 'a' and 'b' in the equation $y = a(b)^x$.

2. Use the First Point to Find 'a'

Substituting the first point $(1, 0.75)$ into the equation:

$$ 0.75 = a(b)^1 $$

This simplifies to:

$$ 0.75 = ab $$

3. Use the Second Point to Create a Second Equation

Substituting the second point $(2, 0.188)$ into the equation:

$$ 0.188 = a(b)^2 $$

This gives us a second equation:

$$ 0.188 = ab^2 $$

4. Set Up the System of Equations

We now have the following system of equations:

1. $0.75 = ab$

2. $0.188 = ab^2$

3. Solve the System of Equations for 'b'

From the first equation, we can express 'a' in terms of 'b':

$$ a = \frac{0.75}{b} $$

Substituting this into the second equation gives:

$$ 0.188 = \left(\frac{0.75}{b}\right) b^2 $$

Which simplifies to:

$$ 0.188 = 0.75b $$

Now solve for 'b':

$$ b = \frac{0.188}{0.75} \approx 0.25067 $$

6. Substitute 'b' Back to Find 'a'

Using the value of 'b' in the first equation:

$$ 0.75 = a(0.25067) $$

Solving for 'a':

$$ a \approx \frac{0.75}{0.25067} \approx 2.99 $$

7. Write the Final Equation

Thus, the equation of the exponential function is approximately:

$$ y \approx 2.99(0.25067)^x $$