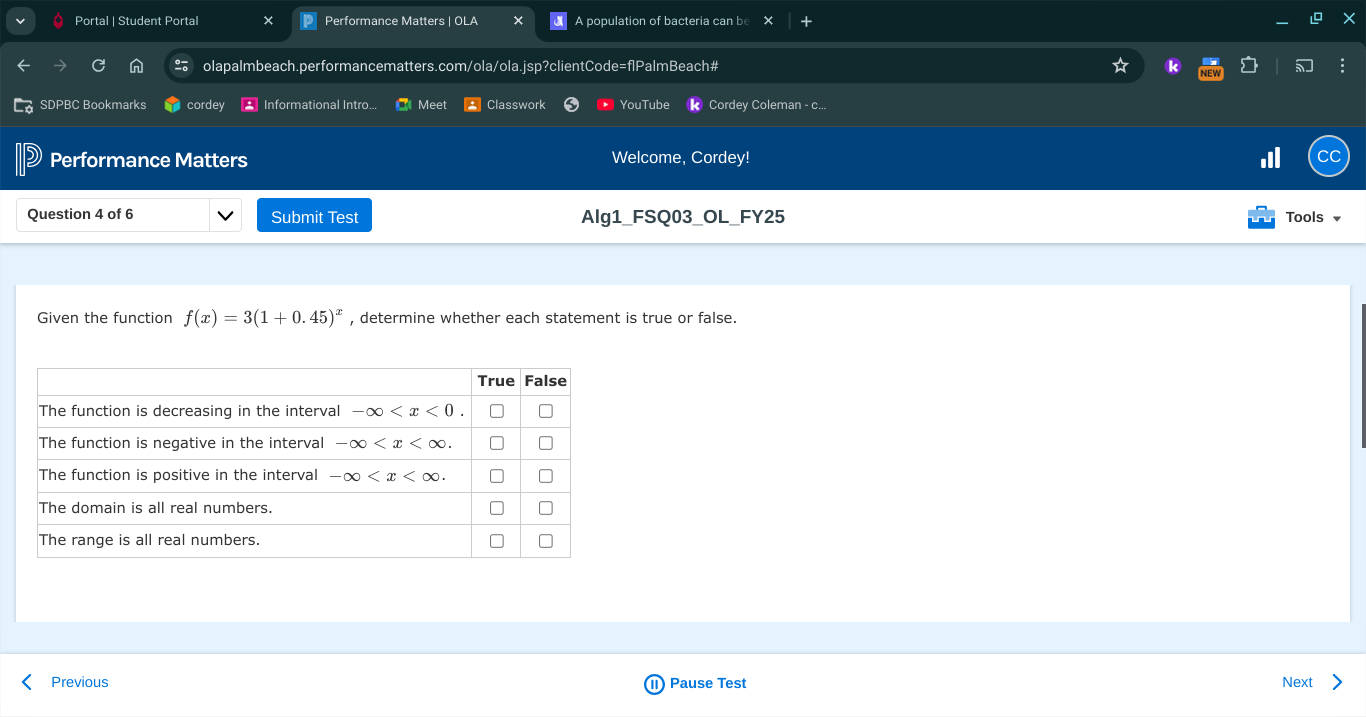
Given the function f(x) = 3(1 + 0.45)^x, determine whether each statement is true or false: The function is decreasing in the interval -∞ < x < 0. The function is negative in the i... Given the function f(x) = 3(1 + 0.45)^x, determine whether each statement is true or false: The function is decreasing in the interval -∞ < x < 0. The function is negative in the interval -∞ < x < ∞. The function is positive in the interval -∞ < x < ∞. The domain is all real numbers. The range is all real numbers.
Understand the Problem
The question is asking to evaluate the given statements about the function f(x) = 3(1 + 0.45)^x, determining whether each statement is true or false based on the properties of the function, such as its behavior in certain intervals, positivity/negativity, and its domain and range.
Answer
- The function is decreasing in the interval \( -\infty < x < 0 \): False - The function is negative in the interval \( -\infty < x < \infty \): False - The function is positive in the interval \( -\infty < x < \infty \): True - The domain is all real numbers: True - The range is all real numbers: False
Answer for screen readers
- The function is decreasing in the interval ( -\infty < x < 0 ): False
- The function is negative in the interval ( -\infty < x < \infty ): False
- The function is positive in the interval ( -\infty < x < \infty ): True
- The domain is all real numbers: True
- The range is all real numbers: False
Steps to Solve
-
Identify the function properties The given function is ( f(x) = 3(1 + 0.45)^x ). This is an exponential function of the form ( f(x) = a(b^x) ), where ( a = 3 ) and ( b = 1.45 ). The base ( b > 1 ) indicates that the function is increasing.
-
Determine the behavior of the function Since ( b = 1.45 ) is greater than 1, the function ( f(x) ) is increasing for all real numbers. Thus,
- The function is not decreasing for any interval.
- Examine the intervals for positivity and negativity For exponential functions of this form:
- When ( x ) is any real number, ( f(x) ) will always yield a positive value because both ( 3 ) and ( (1+0.45)^x ) are positive for all ( x ).
Thus,
- The function is not negative for any interval.
- Evaluate the domain and range The domain of ( f(x) ) is all real numbers because exponential functions are defined for every ( x ).
- The range is ( f(x) > 0 ), which means it includes all positive real numbers.
- Summarize the true/false statements
- The function is decreasing in the interval ( -\infty < x < 0 ): False
- The function is negative in the interval ( -\infty < x < \infty ): False
- The function is positive in the interval ( -\infty < x < \infty ): True
- The domain is all real numbers: True
- The range is all real numbers: False (the range is ( (0, \infty) ))
- The function is decreasing in the interval ( -\infty < x < 0 ): False
- The function is negative in the interval ( -\infty < x < \infty ): False
- The function is positive in the interval ( -\infty < x < \infty ): True
- The domain is all real numbers: True
- The range is all real numbers: False
More Information
The function ( f(x) ) represents exponential growth due to its positive base greater than one. Exponential functions are always positive for any real number input, which influences the outcome of the statements given.
Tips
- Mistaking exponential growth for decay: Remember that if the base of the exponent is greater than 1, the function will always increase.
- Assuming the range includes zero or negative values: All exponential functions of this type will never produce a value less than or equal to zero.
AI-generated content may contain errors. Please verify critical information