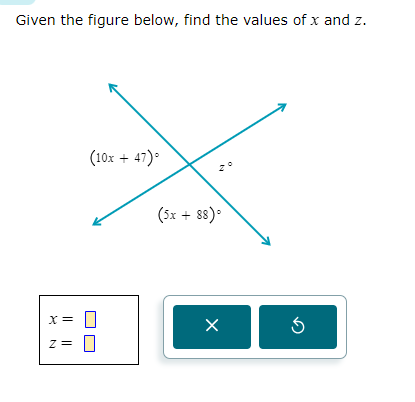
Given the figure below, find the values of x and z.

Understand the Problem

The question is asking for the values of x and z based on the relationships between the angles shown in the figure. Since these angles are across from each other, they are equal, allowing us to set up an equation to solve for both variables.

Answer

$x = 8.2$, $z = 129$

Steps to Solve

Identify Equal Angles

Since the angles are across from each other, they are equal. Therefore, we can set up the equation:

$$(10x + 47) = (5x + 88)$$

Solve for x

Now, simplify and solve for $x$:

First, subtract $5x$ from both sides:

$$10x - 5x + 47 = 88$$

This simplifies to:

$$5x + 47 = 88$$

Next, subtract 47 from both sides:

$$5x = 88 - 47$$

This simplifies to:

$$5x = 41$$

Now, divide both sides by 5:

$$x = \frac{41}{5}$$

Hence,

$$x = 8.2$$

Substitute x to Find z

Now we can find $z$ using the expression $(5x + 88)$:

$$z = 5(8.2) + 88$$

Calculate $5 \times 8.2$:

$$5 \times 8.2 = 41$$

Now add 88:

$$z = 41 + 88$$

So,

$$z = 129$$

The values are:

$x = 8.2$

$z = 129$

More Information

The relationship of opposite angles being equal is fundamental in geometry, which is why we can set up the equation. This property helps solve many angle-related problems.

Tips

Not recognizing equal angles: Make sure to identify which angles are opposite each other.
Arithmetic errors: Double-check calculations when solving for $x$ or $z$.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!