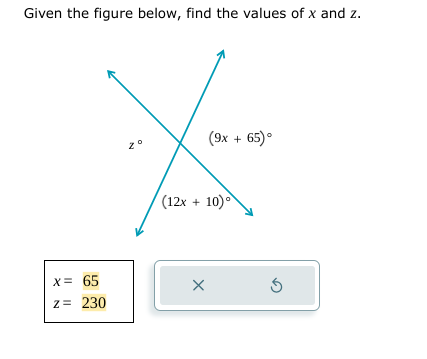
Given the figure below, find the values of x and z.

Understand the Problem

The question is asking to find the values of x and z in a geometry problem involving angles formed by intersecting lines, where two equations are given related to the angles. We will need to set up equations based on the relationships between these angles to solve for x and z.

Answer

$x \approx 18.33$, $z \approx 230$

Steps to Solve

Identify Relationships Between Angles

Given the figure, we have two sets of vertically opposite angles formed by the intersecting lines. The measures of these angles are related:

Angle 1: $z$ (from the left side)
Angle 2: $9x + 65$ (the angle above)
Angle 3: $12x + 10$ (the angle below)

Since vertically opposite angles are equal, we can set up the following equations: $$ z = 9x + 65 $$ $$ z = 12x + 10 $$

Set the Equations Equal to Each Other

Since both equations equal $z$, we can set them equal to one another: $$ 9x + 65 = 12x + 10 $$

Solve for x

To find $x$, rearrange the equation: $$ 9x + 65 - 10 = 12x $$ This simplifies to: $$ 9x + 55 = 12x $$

Now, isolate $x$: $$ 55 = 12x - 9x $$ $$ 55 = 3x $$

Divide both sides by 3: $$ x = \frac{55}{3} = 18.33 $$ (approximately)

Substitute x to Find z

Now that we have $x$, substitute it back into one of the equations for $z$: Using $z = 9x + 65$: $$ z = 9(18.33) + 65 $$ This calculates to: $$ z \approx 165 + 65 $$ $$ z \approx 230 $$

The values are: $x \approx 18.33$ and $z \approx 230$.

More Information

The angles formed by intersecting lines lead to several fundamental properties such as vertically opposite angles being equal. This helps facilitate setting up and solving equations effectively.

Tips

Forgetting to set equations equal: Students often neglect the relationship of vertically opposite angles.
Miscalculating when isolating variables: Care should be taken during algebraic manipulations to avoid simple arithmetic errors.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!