Given the equations x + y = 6 and y = 2x, create tables for each equation using the specified method.
Understand the Problem
The question involves creating tables for two equations: x + y = 6 and y = 2x, which seems to be a method of graphing the functions. The user is demonstrating the calculation of y-values based on different x-values, which suggests a study of graphically representing linear equations.
Answer
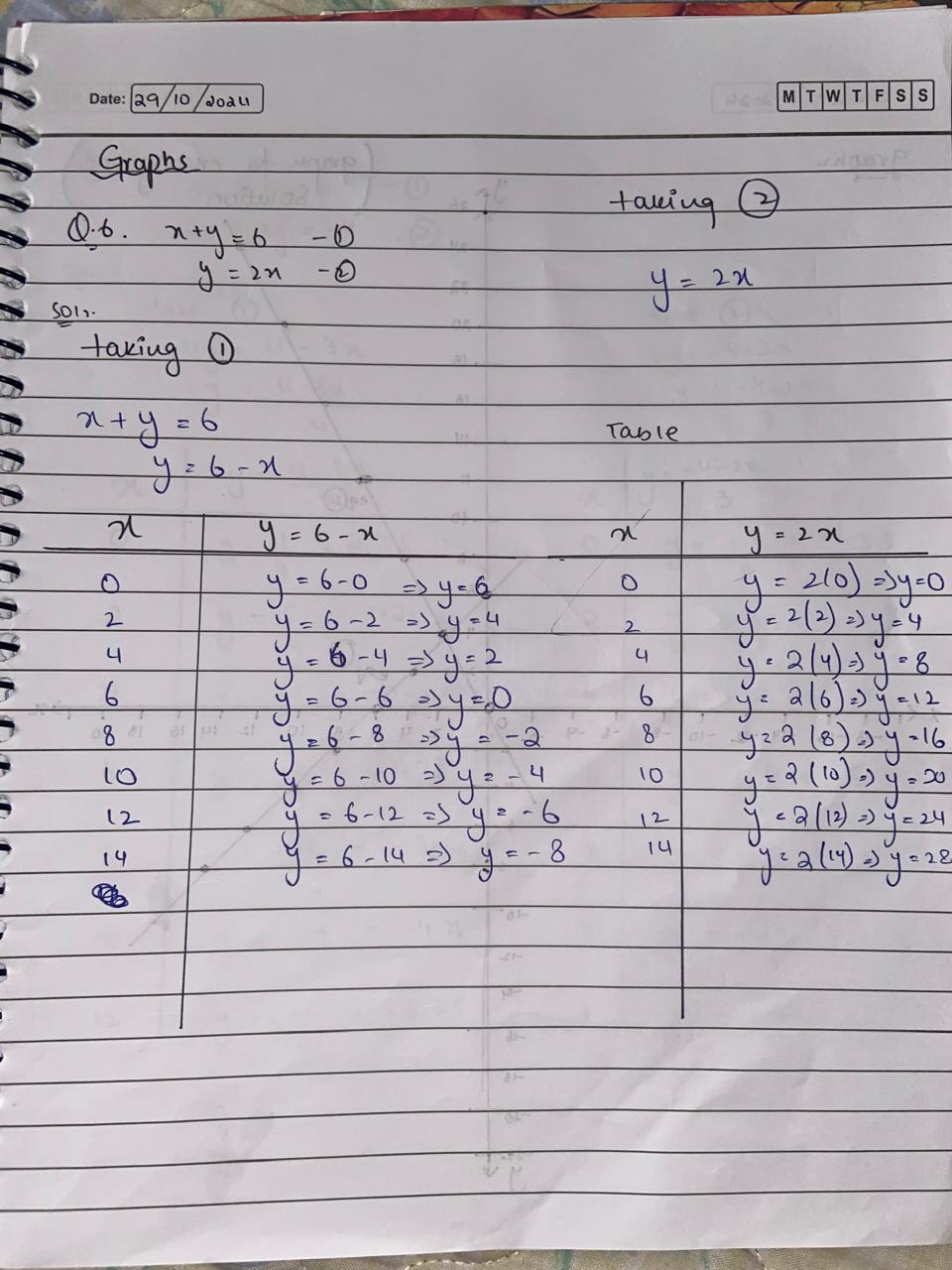
The values calculated for $y$ from the equations are for $y = 6 - x$ as \( (0, 6), (2, 4), (4, 2), (6, 0), (8, -2), (10, -4), (12, -6), (14, -8) \) and for $y = 2x$ as \( (0, 0), (2, 4), (4, 8), (6, 12), (8, 16), (10, 20), (12, 24), (14, 28) \).
Answer for screen readers
The values for the first equation $y = 6 - x$ are:
- ( (0, 6) )
- ( (2, 4) )
- ( (4, 2) )
- ( (6, 0) )
- ( (8, -2) )
- ( (10, -4) )
- ( (12, -6) )
- ( (14, -8) )
The values for the second equation $y = 2x$ are:
- ( (0, 0) )
- ( (2, 4) )
- ( (4, 8) )
- ( (6, 12) )
- ( (8, 16) )
- ( (10, 20) )
- ( (12, 24) )
- ( (14, 28) )
Steps to Solve
-
Equation Setup for $y = 6 - x$
Start with the equation $x + y = 6$. To isolate $y$, rearrange it as:
$$ y = 6 - x $$ -
Create the Table for the First Equation
Choose values for $x$ and calculate $y$:
- For $x = 0$: ( y = 6 - 0 = 6 )
- For $x = 2$: ( y = 6 - 2 = 4 )
- For $x = 4$: ( y = 6 - 4 = 2 )
- For $x = 6$: ( y = 6 - 6 = 0 )
- For $x = 8$: ( y = 6 - 8 = -2 )
- For $x = 10$: ( y = 6 - 10 = -4 )
- For $x = 12$: ( y = 6 - 12 = -6 )
- For $x = 14$: ( y = 6 - 14 = -8 )
-
Equation Setup for $y = 2x$
Next, use the second equation $y = 2x$. This equation is already solved for $y$. -
Create the Table for the Second Equation
Choose values for $x$ and calculate $y$:
- For $x = 0$: ( y = 2(0) = 0 )
- For $x = 2$: ( y = 2(2) = 4 )
- For $x = 4$: ( y = 2(4) = 8 )
- For $x = 6$: ( y = 2(6) = 12 )
- For $x = 8$: ( y = 2(8) = 16 )
- For $x = 10$: ( y = 2(10) = 20 )
- For $x = 12$: ( y = 2(12) = 24 )
- For $x = 14$: ( y = 2(14) = 28 )
The values for the first equation $y = 6 - x$ are:
- ( (0, 6) )
- ( (2, 4) )
- ( (4, 2) )
- ( (6, 0) )
- ( (8, -2) )
- ( (10, -4) )
- ( (12, -6) )
- ( (14, -8) )
The values for the second equation $y = 2x$ are:
- ( (0, 0) )
- ( (2, 4) )
- ( (4, 8) )
- ( (6, 12) )
- ( (8, 16) )
- ( (10, 20) )
- ( (12, 24) )
- ( (14, 28) )
More Information
The two equations represent linear functions. The first equation, $y = 6 - x$, has a y-intercept of 6 and a slope of -1, while the second equation, $y = 2x$, has a slope of 2 and passes through the origin. The tables created can be used to graph these lines on a coordinate plane.
Tips
- Incorrect rearrangement of equations: Ensure that you isolate $y$ correctly without making arithmetic mistakes.
- Not choosing enough $x$ values: Selecting a broader range of $x$ values can give a fuller picture of the function's behavior.
AI-generated content may contain errors. Please verify critical information