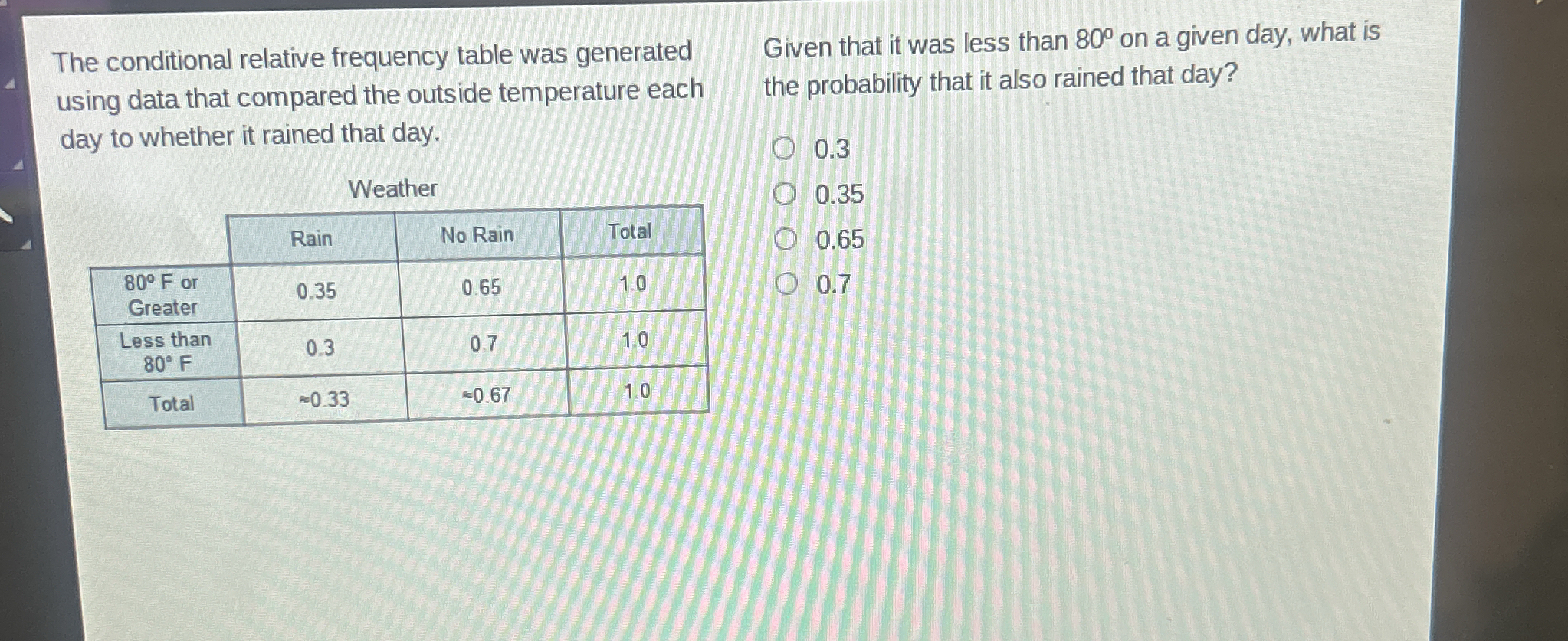
Given that it was less than 80 degrees Fahrenheit on a given day, what is the probability that it also rained that day?

Understand the Problem

The question is asking for the conditional probability of it raining given that the outside temperature was less than 80°F. It requires using the provided conditional relative frequency table to find the answer.

Answer

The probability that it rained given that the temperature was less than 80°F is $0.3$.

Steps to Solve

Identify relevant data from the table

From the table, we need the probabilities of it raining when the temperature is less than 80°F. According to the table:

Probability of Rain when the temperature is less than 80°F: $P(\text{Rain} | \text{Less than } 80°F) = 0.3$

Understand the total context for conditional probability

The conditional probability is defined as:

$$ P(A | B) = \frac{P(A \cap B)}{P(B)} $$

Where:

$A$ is the event of it raining.
$B$ is the event that the temperature is less than 80°F.

But in this case, we directly have the conditional probability from the table.

Extract the needed probability

From our observations:

The probability of rain on a day with less than 80°F temperature has been directly provided as $P(\text{Rain} | \text{Less than } 80°F) = 0.3$.

Final confirmation of the selected option

Given it was less than 80°F on a given day, the relevant probability that it also rained that day is $0.3$.

The probability that it rained given that the temperature was less than 80°F is $0.3$.

More Information

Conditional probability helps us understand how the occurrence of one event affects the likelihood of another. In this case, we see how temperature influences rainfall.

Tips

Confusing the total probabilities (like summing probabilities) with conditional probabilities. Remember, we are looking only at specific conditions.
Misreading values from the table; be careful to always check which condition applies.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!