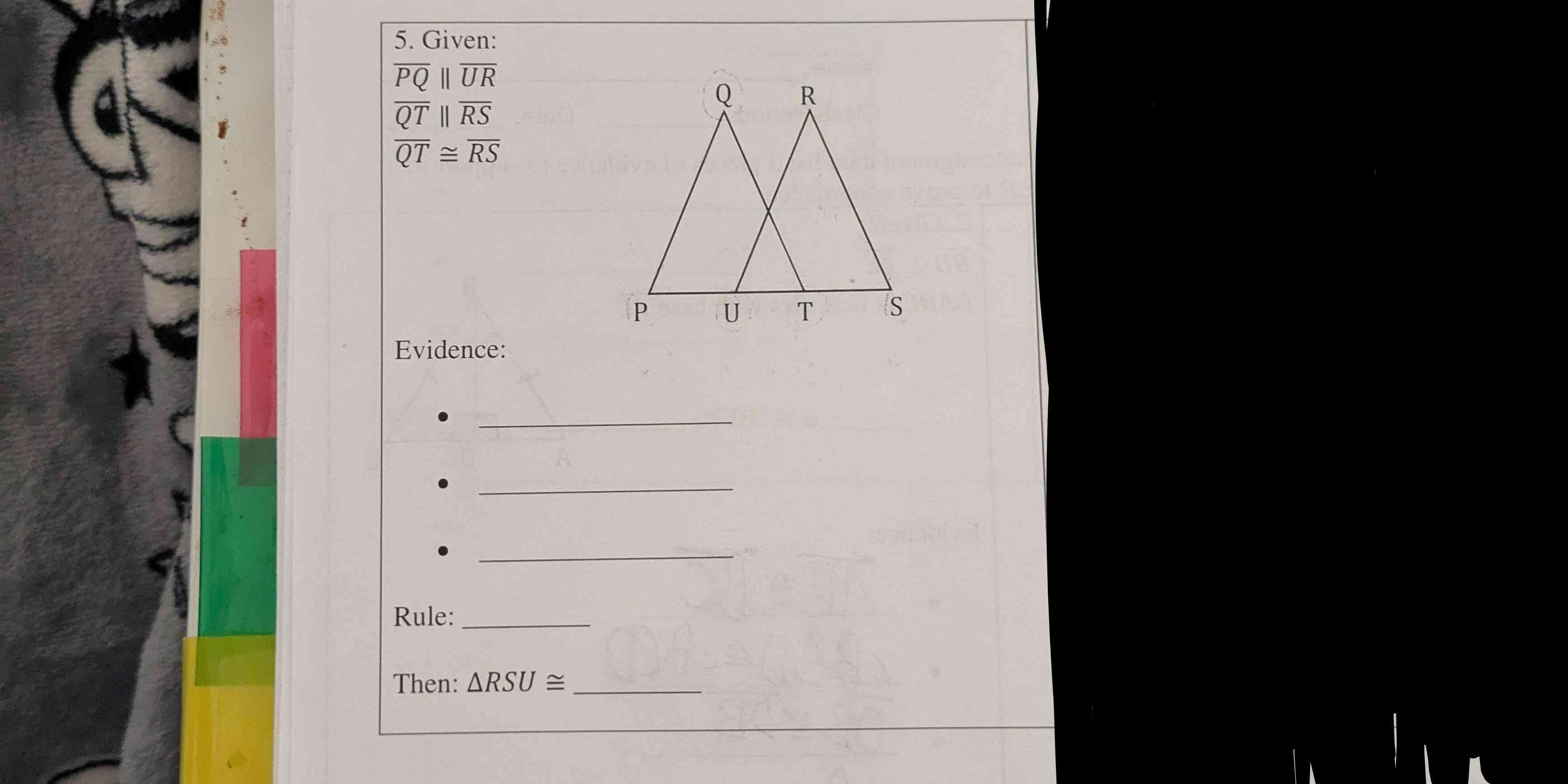
Given: PQ || UR, QT || RS, QT ≅ RS. Evidence: ... Rule: ... Then: ΔRSU ≅ ...
Understand the Problem
The question provides a geometric scenario with parallel lines and two triangles. It asks for evidence and a rule to conclude that the triangles ΔRSU and another triangle are congruent.
Answer
$$ \triangle RSU \cong \triangle PQU $$
Answer for screen readers
$$ \triangle RSU \cong \triangle PQU $$
Steps to Solve
- Identify given information
From the problem, we know that:
- Lines $PQ$ and $UR$ are parallel ($PQ \parallel UR$).
- Segments $QT$ and $RS$ are also parallel ($QT \parallel RS$).
- The lengths of segments $QT$ and $RS$ are equal ($QT \cong RS$).
- Understanding triangle ΔRSU
We need to show that triangle ΔRSU is congruent to another triangle. The triangles sharing sides or angles will help in the congruency proof.
- Utilize properties of parallel lines
Since $PQ \parallel UR$, we can establish that the alternate interior angles are equal. Therefore, we have: $$ \angle PQU \cong \angle RUS $$
- Show congruence criteria
We will use the Angle-Side-Angle (ASA) congruence criterion. We already have:
- One pair of angles from the parallel lines: $ \angle PQU \cong \angle RUS $.
- One side is given as equal: $QT \cong RS$.
- Conclude the congruence
By the ASA criterion, we can conclude: $$ \triangle RSU \cong \triangle PQU $$
Thus, fill in the blanks for evidence and rule:
- Evidence: $ \angle PQU \cong \angle RUS $ (alternate interior angles), $QT \cong RS$ (given side).
- Rule: ASA.
$$ \triangle RSU \cong \triangle PQU $$
More Information
The congruence of triangles is a fundamental concept in geometry which ensures that two triangles are identical in shape and size under certain conditions (like having equal corresponding sides and angles).
Tips
- Confusing congruence criteria (e.g., using SSS instead of ASA).
- Forgetting to account for all necessary angles or sides when proving congruence.
AI-generated content may contain errors. Please verify critical information