Given points E(0, 1) and F(2√3, 7), find the magnitude and the unit vector.

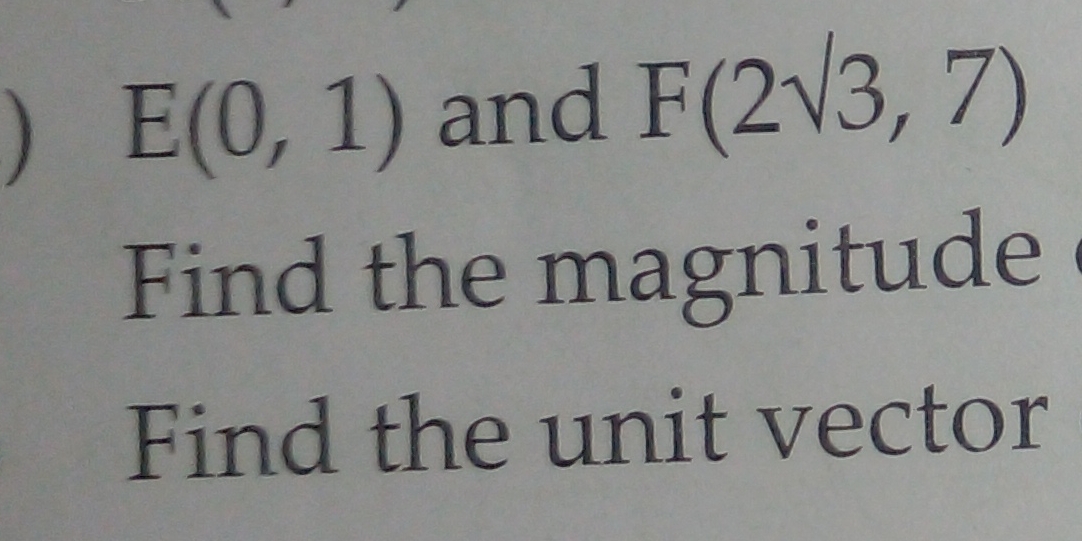
Understand the Problem

The question is asking us to find the magnitude and the unit vector, given two points E and F. We will first find the vector EF, then calculate its magnitude, and finally find the unit vector by dividing the vector EF by its magnitude.

Answer

Magnitude: $4\sqrt{3}$ Unit Vector: $\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)$

Steps to Solve

Find the vector $\vec{EF}$ To find the vector $\vec{EF}$, we subtract the coordinates of point E from the coordinates of point F. $$ \vec{EF} = F - E = (2\sqrt{3} - 0, 7 - 1) = (2\sqrt{3}, 6) $$
Calculate the magnitude of $\vec{EF}$ The magnitude of a vector $(a, b)$ is given by $\sqrt{a^2 + b^2}$. Therefore, the magnitude of $\vec{EF}$ is: $$ |\vec{EF}| = \sqrt{(2\sqrt{3})^2 + 6^2} = \sqrt{(4 \cdot 3) + 36} = \sqrt{12 + 36} = \sqrt{48} $$ $$ |\vec{EF}| = \sqrt{16 \cdot 3} = 4\sqrt{3} $$
Find the unit vector $\hat{u}_{EF}$ The unit vector is found by dividing the vector by its magnitude: $$ \hat{u}{EF} = \frac{\vec{EF}}{|\vec{EF}|} = \frac{(2\sqrt{3}, 6)}{4\sqrt{3}} = \left(\frac{2\sqrt{3}}{4\sqrt{3}}, \frac{6}{4\sqrt{3}}\right) $$ $$ \hat{u}{EF} = \left(\frac{1}{2}, \frac{3}{2\sqrt{3}}\right) = \left(\frac{1}{2}, \frac{3\sqrt{3}}{2 \cdot 3}\right) = \left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right) $$

Magnitude: $4\sqrt{3}$ Unit Vector: $\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)$

More Information

The magnitude represents the length of the vector from point E to point F. The unit vector points in the same direction as the original vector but has a magnitude of 1.

Tips

A common mistake is not simplifying the radical correctly when calculating the magnitude, or not rationalizing the denominator correctly when calculating the unit vector. Also, one might mix up the order of subtraction when finding the vector $\vec{EF}$ (i.e., E - F instead of F - E).

AI-generated content may contain errors. Please verify critical information

Thank you for voting!