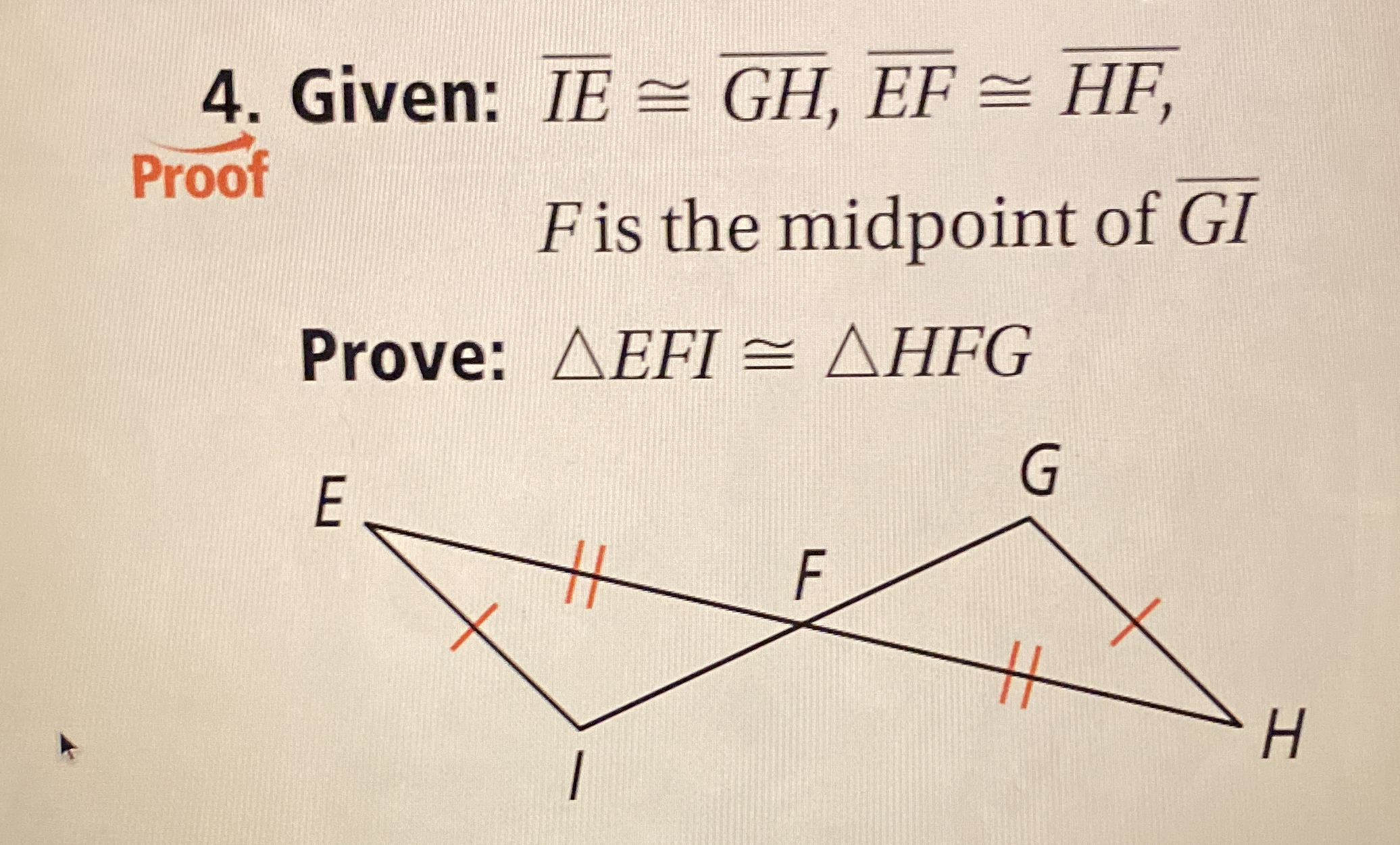
Given: IE ≅ GH, EF ≅ HF, F is the midpoint of GI. Prove: ΔEFI ≅ ΔHFG.
Understand the Problem
The question is asking for a geometric proof that involves two triangles, given specific conditions about their sides and a midpoint. The objective is to prove that the two triangles are congruent.
Answer
$$ \Delta EFI \cong \Delta HFG $$
Answer for screen readers
$$ \Delta EFI \cong \Delta HFG $$
Steps to Solve
- Identify Given Information
We have the following congruences and midpoint:
- $IE \cong GH$
- $EF \cong HF$
- $F$ is the midpoint of $GI$, which implies that $GF \cong FI$.
- Construct Triangles
We are tasked with proving that triangles $\Delta EFI$ and $\Delta HFG$ are congruent, using the information titled in the given statement.
- Apply the Side-Side-Side (SSS) Congruence Criterion
- Since $F$ is the midpoint of $GI$, we have:
$$ GF \cong FI $$
Thus, we can establish three pairs of congruent sides:
- $IE \cong GH$
- $EF \cong HF$
- $GF \cong FI$
- Conclude by SSS Criterion
By the SSS criterion, if all corresponding sides of two triangles are congruent, then the triangles are congruent:
$$ \Delta EFI \cong \Delta HFG $$
$$ \Delta EFI \cong \Delta HFG $$
More Information
The proof uses the SSS (Side-Side-Side) Congruence Criterion, which states that if three sides of one triangle are equal to three sides of another triangle, then the triangles are congruent. Midpoints also play a crucial role in establishing one of the side congruences.
Tips
- Forgetting the midpoint information: Always ensure you acknowledge midpoints, as they simplify congruency proofs.
- Miscalculating side lengths or forgetting to state congruences: Be meticulous in writing down all congruences step-by-step to avoid missing important information.
AI-generated content may contain errors. Please verify critical information