Given: E is the midpoint of AB, E is the midpoint of CD. Prove: ΔAEC ≅ ΔBED.
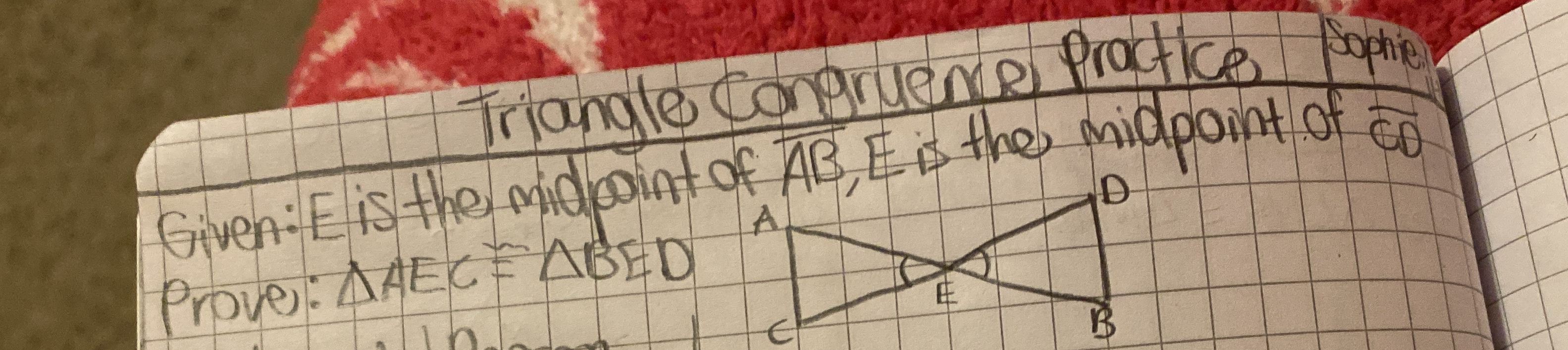
Understand the Problem
The question is asking to prove that two triangles, ΔAEC and ΔBED, are congruent given that E is the midpoint of segment AB and E is also the midpoint of segment CD. This involves using properties of triangles and midpoint relationships to establish congruence.
Answer
$\Delta AEC \cong \Delta BED$
Answer for screen readers
$$ \Delta AEC \cong \Delta BED $$
Steps to Solve
-
Identify Given Information
We know that $E$ is the midpoint of segments $AB$ and $CD$. Thus, we have:
$$ AE = EB \text{ and } CE = ED $$ -
Use Midpoint Properties
Since $E$ is the midpoint, we can express segment lengths:
Let $AE = x$ and $CE = y$. Then,
$$ EB = x \text{ and } ED = y $$ -
Establish Corresponding Parts
We recognize that the segments $AE$ and $EB$ are equal, as are $CE$ and $ED$. Therefore, we can assert that:
- $AE = EB$
- $CE = ED$
-
Consider Vertical Angles
The angles $\angle AEC$ and $\angle BED$ are vertical angles. By the Vertical Angles Theorem, we know that vertical angles are congruent:
$$ \angle AEC \cong \angle BED $$ -
Apply the Triangle Congruence Theorem
We can now apply the Side-Angle-Side (SAS) Triangle Congruence Postulate:
Since $AE = EB$, $CE = ED$, and $\angle AEC \cong \angle BED$, we can conclude:
$$ \Delta AEC \cong \Delta BED $$
$$ \Delta AEC \cong \Delta BED $$
More Information
The congruence of the triangles indicates they have the same shape and size, which means corresponding angles and sides are equal. This congruence can be useful in various applications, such as solving for unknown lengths or angles in geometric problems.
Tips
- Forgetting to mention that vertical angles are congruent can lead to incomplete proof.
- Misinterpreting the midpoint information; ensure that all sides are correctly labeled and considered.
AI-generated content may contain errors. Please verify critical information