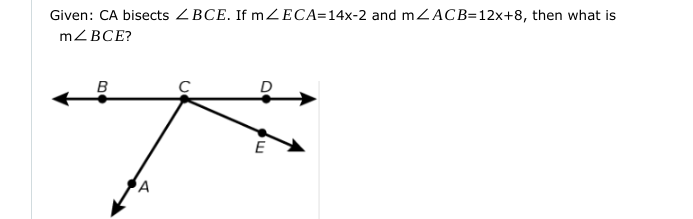
Given: CA bisects angle BCE. If m∠ECA = 14x - 2 and m∠ACB = 12x + 8, then what is m∠BCE?
Understand the Problem
The question is asking to find the measure of angle BCE given that CA bisects angle BCE. We are provided with the measurements of angles ECA and ACB in terms of x, and we need to set up an equation based on the property of angle bisection.
Answer
The measure of angle \( BCE \) is \( 136^\circ \).
Answer for screen readers
The measure of angle ( BCE ) is ( 136^\circ ).
Steps to Solve
-
Write the angle bisector property
Since line segment CA bisects angle BCE, we know that:
$$ m\angle ECA = m\angle ACB $$ -
Set up the equation
We can substitute the given expressions for the angles into the equation:
$$ 14x - 2 = 12x + 8 $$ -
Solve for x
To isolate (x), subtract (12x) from both sides:
$$ 14x - 12x - 2 = 8 $$
This simplifies to:
$$ 2x - 2 = 8 $$
Next, add 2 to both sides:
$$ 2x = 10 $$
Now, divide by 2:
$$ x = 5 $$ -
Find the measures of the angles
Substitute (x) back into either equation to find the measure of the angles:
Using ( m\angle ECA ):
$$ m\angle ECA = 14(5) - 2 = 70 - 2 = 68 $$ -
Calculate m∠BCE
Since ( m\angle BCE = 2 \times m\angle ECA ), we multiply:
$$ m\angle BCE = 2 \times 68 = 136 $$
The measure of angle ( BCE ) is ( 136^\circ ).
More Information
The property of angle bisectors states that if a line bisects an angle, the two resulting angles are equal. In this case, knowing two expressions for the angles allowed us to create an equation and solve for the unknown.
Tips
- Forgetting to set the equations equal to each other when using the angle bisector property.
- Miscalculating when solving for (x), such as errors in subtraction or division.
AI-generated content may contain errors. Please verify critical information