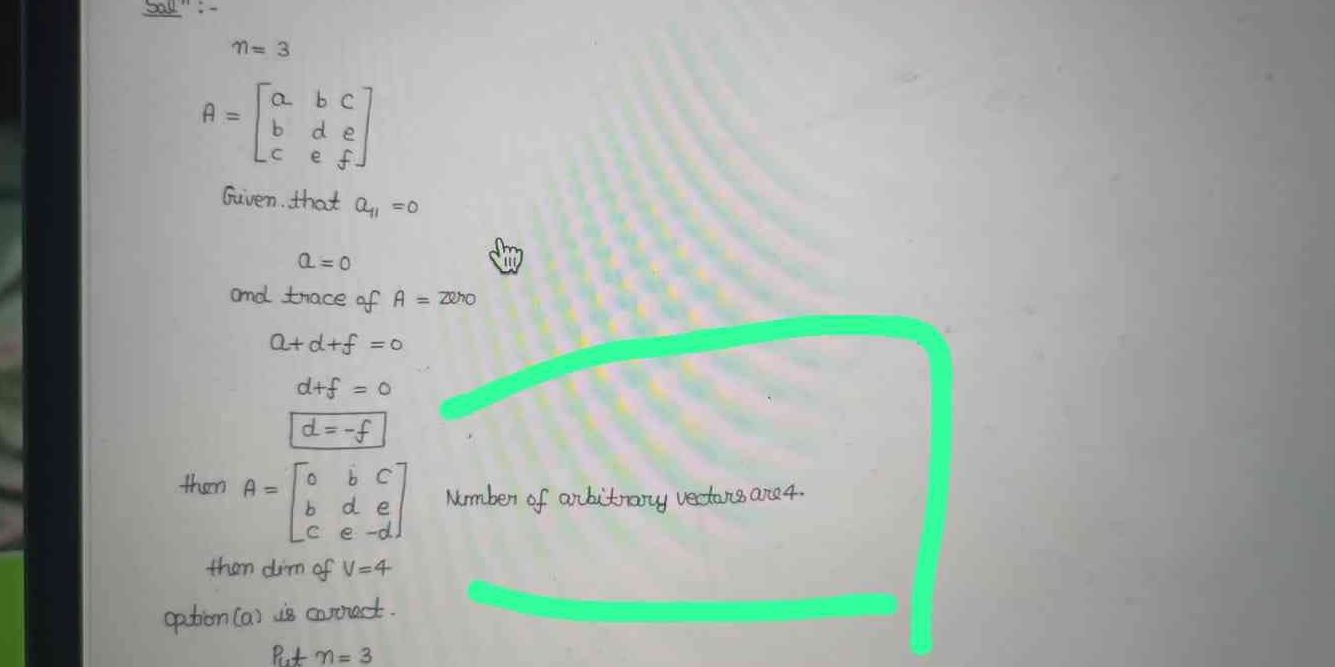
Given a matrix A defined as A = [[a, b, c], [b, d, e], [c, e, f]] with conditions that a1 = 0, a = 0, and trace of A = 0, determine the number of arbitrary vectors when it's stated... Given a matrix A defined as A = [[a, b, c], [b, d, e], [c, e, f]] with conditions that a1 = 0, a = 0, and trace of A = 0, determine the number of arbitrary vectors when it's stated that dim V = 4. Is option (a) correct?
Understand the Problem
The question discusses a matrix A and involves calculations related to its determinant and trace, specifically focusing on the number of arbitrary vectors, which connects to concepts in linear algebra. The objective is to derive or confirm the number of arbitrary vectors given the conditions in the problem statement.
Answer
The number of arbitrary vectors is 4.
Answer for screen readers
The number of arbitrary vectors is 4.
Steps to Solve
- Understanding the matrix conditions
Given the matrix ( A = \begin{bmatrix} a & b & c \ d & e & f \ g & h & i \end{bmatrix} ) and the conditions that ( a_1 = 0 ), ( a = 0 ), and the trace of ( A = 0 ). The trace of a matrix is the sum of its diagonal elements, so:
$$ a + d + f = 0 $$
- Simplifying with known values
Substituting ( a = 0 ) into the trace equation gives:
$$ 0 + d + f = 0 $$
which simplifies to:
$$ d + f = 0 $$
This leads to the conclusion that:
$$ d = -f $$
- Rewriting the matrix
Now substituting ( d = -f ) into the matrix yields:
$$ A = \begin{bmatrix} 0 & b & c \ -f & e & f \ g & h & i \end{bmatrix} $$
- Examining the dimensions of the vector space
This matrix has 5 independent variables: ( b, c, e, f, g, h, i ). Therefore, the dimension of the vector space spanned by these arbitrary vectors is:
$$ \text{dim}(V) = 4 $$
since one of the degrees of freedom is removed due to the conditions applied to the values of matrix ( A ).
- Final observation on arbitrary vectors
From the dimension calculated, we conclude that the number of arbitrary vectors in the corresponding vector space is 4.
The number of arbitrary vectors is 4.
More Information
This problem involves understanding the properties of determinants and traces of matrices within the context of linear algebra, revealing how constraints can reduce the degrees of freedom in a system.
Tips
- Miscalculating the trace by forgetting to consider each diagonal element.
- Overlooking that setting one parameter to zero reduces the overall dimensionality of the space.
AI-generated content may contain errors. Please verify critical information