Given A, B, C ⊂ U where |U| = 90, |A ∩ C| = 15, |C ∩ B| = 11, |A ∩ B ∩ C| = 11, |A ∩ B| = 13, |A| = |B| = |C| = 30 what is: (a) |A ∪ B ∪ C| equal to? (b) |(A ∪ B ∪ C)ᶜ| equal to? Given A, B, C ⊂ U where |U| = 90, |A ∩ C| = 15, |C ∩ B| = 11, |A ∩ B ∩ C| = 11, |A ∩ B| = 13, |A| = |B| = |C| = 30 what is: (a) |A ∪ B ∪ C| equal to? (b) |(A ∪ B ∪ C)ᶜ| equal to?
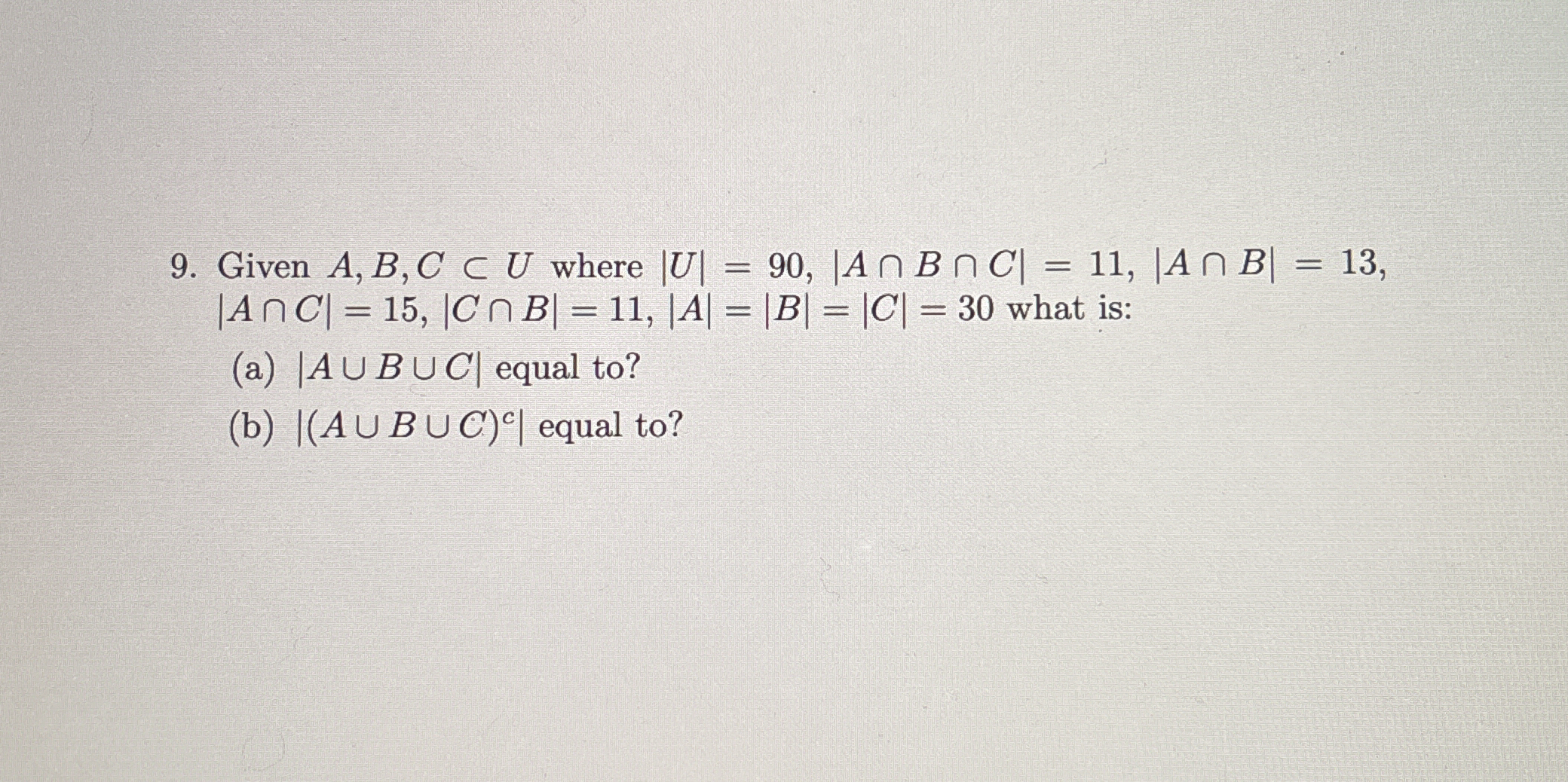
Understand the Problem
The question requires us to find the cardinality of the union of sets A, B, and C, as well as the cardinality of the complement of that union, using provided information about the sizes of various intersections and the total size of the universal set.
Answer
(a) \( 62 \), (b) \( 28 \)
Answer for screen readers
(a) ( |A \cup B \cup C| = 62 )
(b) ( |(A \cup B \cup C)^c| = 28 )
Steps to Solve
- Understanding set notation and formula We will use the principle of inclusion-exclusion to calculate the cardinality of the union of sets A, B, and C. The formula is given by:
$$ |A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C| $$
- Plugging in the values From the problem, we know:
- ( |A| = 30 )
- ( |B| = 30 )
- ( |C| = 30 )
- ( |A \cap B| = 13 )
- ( |A \cap C| = 15 )
- ( |B \cap C| = 11 )
- ( |A \cap B \cap C| = 11 )
Now substitute these values into the formula:
$$ |A \cup B \cup C| = 30 + 30 + 30 - 13 - 15 - 11 + 11 $$
- Calculating the cardinality of the union Now let's simplify the equation step by step:
$$ |A \cup B \cup C| = 90 - 13 - 15 - 11 + 11 $$
Calculating it step-by-step:
- ( 90 - 13 = 77 )
- ( 77 - 15 = 62 )
- ( 62 - 11 = 51 )
- ( 51 + 11 = 62 )
Therefore,
$$ |A \cup B \cup C| = 62 $$
- Finding complement of the union The complement of the union is given by:
$$ |(A \cup B \cup C)^c| = |U| - |A \cup B \cup C| $$
Given that ( |U| = 90 ):
$$ |(A \cup B \cup C)^c| = 90 - 62 $$
- Final calculation for the complement Calculating the complement:
$$ |(A \cup B \cup C)^c| = 90 - 62 = 28 $$
(a) ( |A \cup B \cup C| = 62 )
(b) ( |(A \cup B \cup C)^c| = 28 )
More Information
The principle of inclusion-exclusion allows us to accurately find the size of the union of multiple sets by accounting for overlaps. Understanding the sizes of intersections is crucial for accurate calculations.
Tips
- Forgetting terms in the inclusion-exclusion formula: Make sure to include all intersections and avoid omitting any terms.
- Miscalculating values: Carefully perform arithmetic operations step-by-step to prevent errors.
AI-generated content may contain errors. Please verify critical information