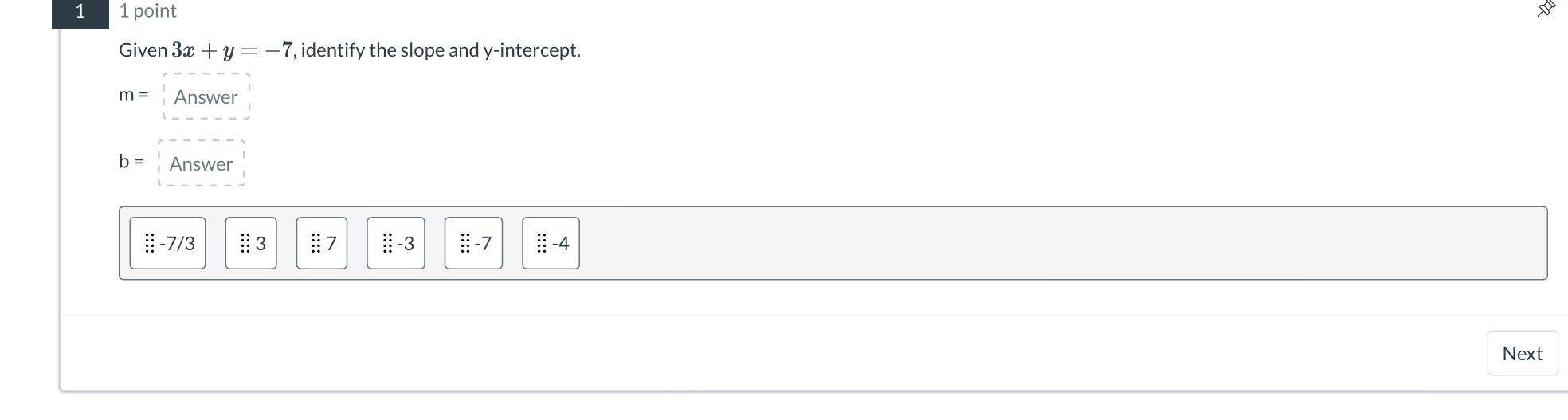
Given 3x + y = -7, identify the slope and y-intercept.
Understand the Problem
The question is asking to identify the slope and y-intercept from the linear equation given in standard form, 3x + y = -7. To solve it, we need to convert the equation to slope-intercept form (y = mx + b) and extract the values for m (slope) and b (y-intercept).
Answer
$m = -3$, $b = -7$
Answer for screen readers
The slope is $m = -3$ and the y-intercept is $b = -7$.
Steps to Solve
- Convert to Slope-Intercept Form
Transform the standard form equation $3x + y = -7$ to slope-intercept form, which is $y = mx + b$.
Start by isolating $y$: $$ y = -3x - 7 $$
- Identify the Slope (m)
From the equation $y = -3x - 7$, the coefficient of $x$ represents the slope $m$.
Thus, $$ m = -3 $$
- Identify the Y-Intercept (b)
In the equation $y = -3x - 7$, the constant term is the y-intercept $b$.
So, $$ b = -7 $$
The slope is $m = -3$ and the y-intercept is $b = -7$.
More Information
The slope indicates that for every 1 unit increase in $x$, $y$ decreases by 3 units. The y-intercept means the line crosses the y-axis at -7.
Tips
- Forgetting to isolate $y$ properly when converting to slope-intercept form.
- Misidentifying the slope as the y-intercept or vice versa.
AI-generated content may contain errors. Please verify critical information