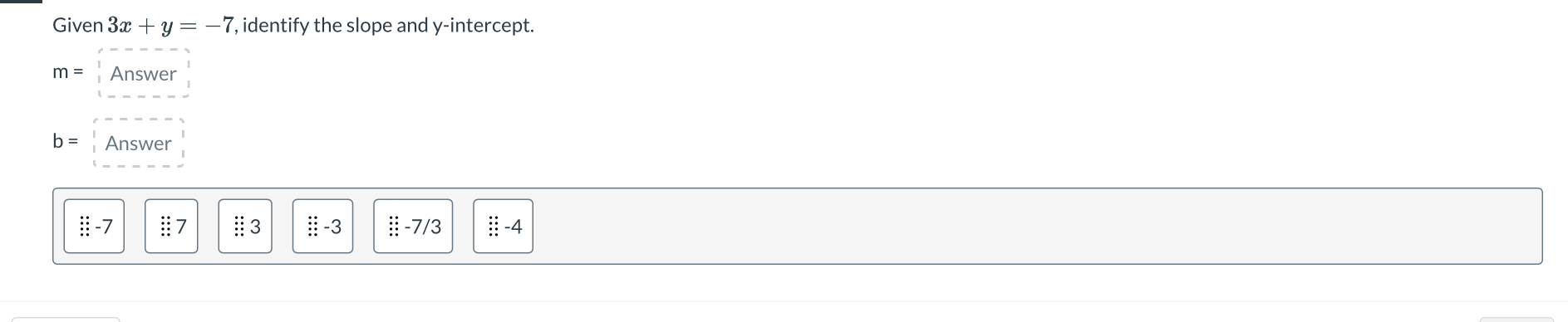
Given 3x + y = -7, identify the slope and y-intercept.
Understand the Problem
The question is asking to identify the slope (m) and y-intercept (b) of the linear equation given in the form 3x + y = -7. To do this, we will rearrange the equation into the slope-intercept form (y = mx + b).
Answer
m = $-3$, b = $-7$
Answer for screen readers
m = $-3$
b = $-7$
Steps to Solve
- Rearranging the Equation to y = mx + b Form
Start with the given equation: $$ 3x + y = -7 $$ Subtract $3x$ from both sides to isolate $y$: $$ y = -3x - 7 $$
- Identifying the Slope (m) and Y-Intercept (b)
Now that the equation is in the form $y = mx + b$, identify the slope and y-intercept:
- The slope $m$ is the coefficient of $x$, which is $-3$.
- The y-intercept $b$ is the constant term, which is $-7$.
m = $-3$
b = $-7$
More Information
The slope of $-3$ indicates that for every unit increase in $x$, $y$ decreases by 3 units. The y-intercept of $-7$ tells us that the line crosses the y-axis at the point (0, -7).
Tips
- Forgetting to isolate $y$ properly by not correctly rearranging the equation can lead to wrong values for $m$ and $b$.
- Misidentifying the slope and intercept after rearranging; double-checking the coefficients is key.
AI-generated content may contain errors. Please verify critical information