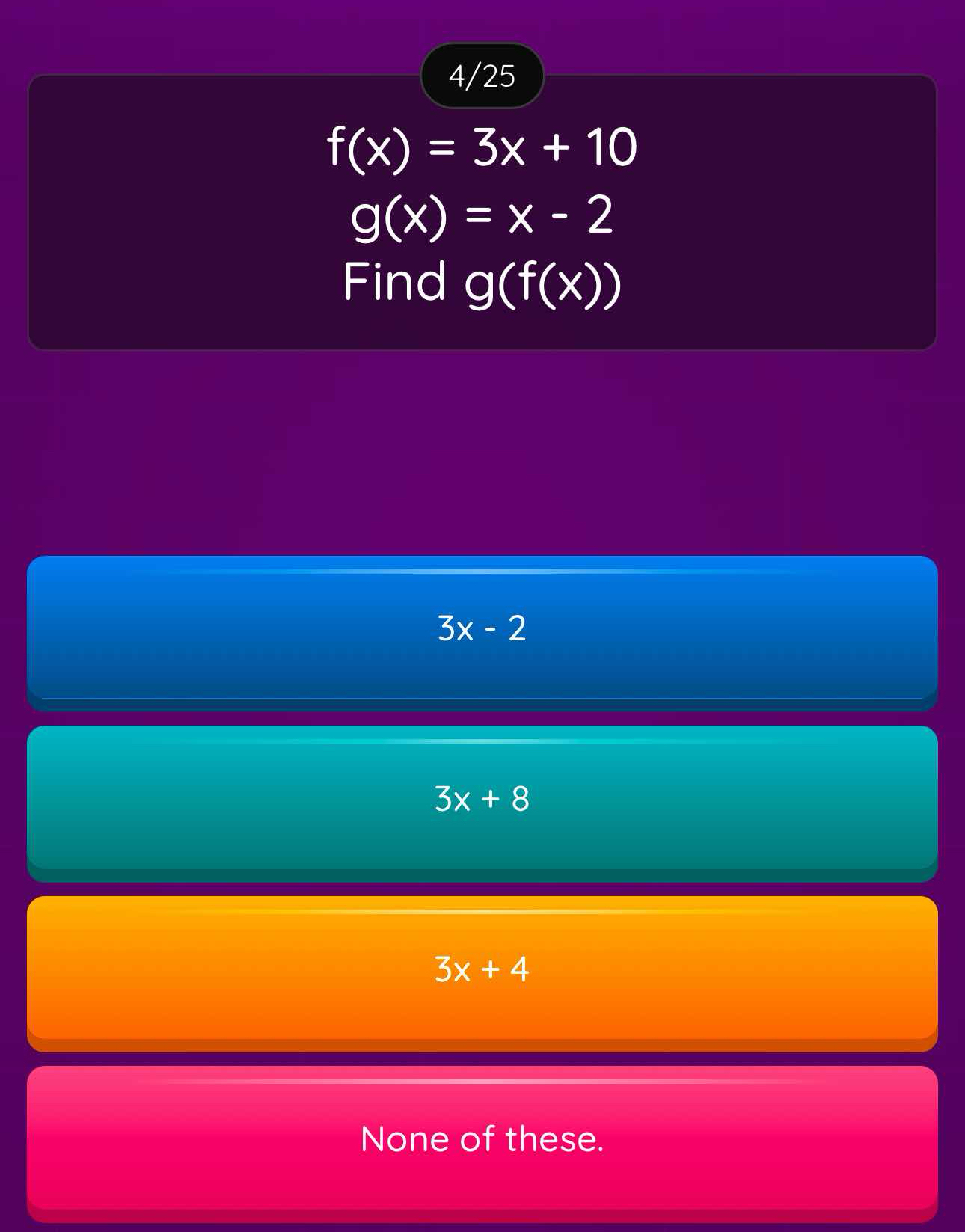
f(x) = 3x + 10; g(x) = x - 2. Find g(f(x)).

Understand the Problem

The question is asking for the composition of two functions, f(x) and g(x). Specifically, we need to find g(f(x)), which involves substituting the output of f(x) into g(x). This will involve evaluating f(x) first and then finding g of that result.

Answer

$3x + 8$

Steps to Solve

Evaluate f(x)

First, we find the expression for $f(x)$. Given that $f(x) = 3x + 10$, we will use this in the next step.

Substitute f(x) into g(x)

Next, we need to find $g(f(x))$. We substitute the expression we found for $f(x)$ into $g(x)$.

We know that $g(x) = x - 2$. Therefore, we substitute $f(x)$:

$$ g(f(x)) = g(3x + 10) $$

Now, we replace $x$ in $g(x)$ with $3x + 10$:

$$ g(3x + 10) = (3x + 10) - 2 $$

Simplify the expression

Now we simplify:

$$ g(3x + 10) = 3x + 10 - 2 = 3x + 8 $$

Thus, we have found that

$$ g(f(x)) = 3x + 8 $$

The final answer is $3x + 8$.

More Information

The composition of functions is a way to combine two functions where the output of one becomes the input of the other. Here, we combined $f(x)$ and $g(x)$ to find $g(f(x))$.

Tips

Misunderstanding what the composition means; it's crucial to ensure you substitute correctly.
Failing to simplify after substitution; always simplify the expression completely.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!