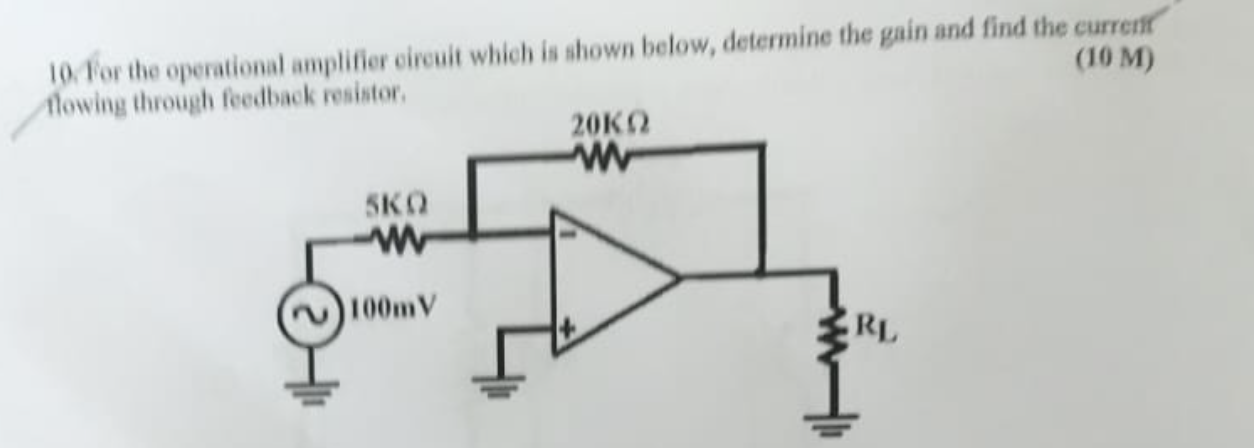
For the operational amplifier circuit which is shown below, determine the gain and find the current flowing through feedback resistor.

Steps to Solve

1. Determine the Gain of the Amplifier

For a non-inverting operational amplifier configuration, the gain ($A_v$) can be calculated using the formula:

$$ A_v = 1 + \frac{R_f}{R_{in}} $$

where ( R_f ) is the feedback resistor (20 kΩ) and ( R_{in} ) is the input resistor (5 kΩ).

Substituting the values:

$$ A_v = 1 + \frac{20,000 , \Omega}{5,000 , \Omega} $$

2. Calculate Input and Output Values

First, calculate the gain:

$$ A_v = 1 + 4 = 5 $$

Now, the output voltage ($V_{out}$) can be determined using the input voltage ($V_{in} = 100 , mV$):

$$ V_{out} = A_v \cdot V_{in} $$

Substituting the values:

$$ V_{out} = 5 \cdot 100 , mV $$

3. Calculate Output Voltage

Now, calculate the output voltage:

$$ V_{out} = 500 , mV $$

4. Current Through the Feedback Resistor

To find the current ($I_f$) flowing through the feedback resistor ($R_f$ = 20 kΩ), we use Ohm's Law:

$$ I_f = \frac{V_{out}}{R_f} $$

Substituting the known values:

$$ I_f = \frac{500 , mV}{20,000 , \Omega} $$

5. Calculate the Current

Now, calculate the current through the feedback resistor:

$$ I_f = \frac{0.5 , V}{20,000 , \Omega} = 0.000025 , A = 25 , \mu A $$