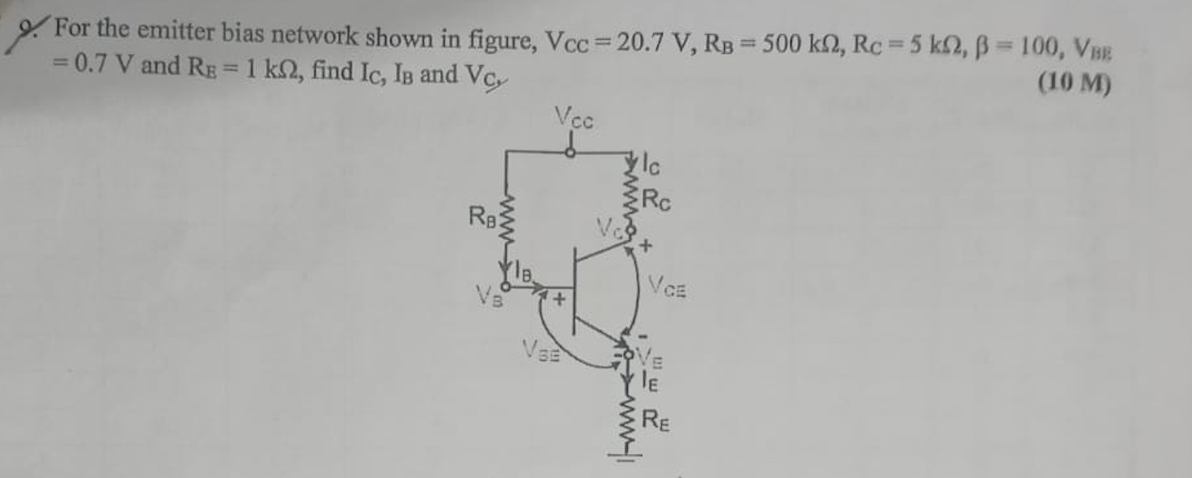
For the emitter bias network shown in figure, Vcc = 20.7 V, RB = 500 kΩ, RC = 5 kΩ, β = 100, VBE = 0.7 V and RE = 1 kΩ, find IC, IB and VC.
Understand the Problem
The question is asking to calculate the values of collector current (IC), base current (IB), and collector voltage (VC) for a transistor circuit with given parameters. The high-level approach involves using the transistor biasing equations and Ohm's law to solve for these currents and voltages based on the provided circuit information.
Answer
$IC \approx 19.6 \, \text{mA}, \, IB \approx 196 \, \mu \text{A}, \, VC \approx 16.8 \, V$
Answer for screen readers
- Collector Current, $I_C \approx 19.6 , mA$
- Base Current, $I_B \approx 196 , \mu A$
- Collector Voltage, $V_C \approx 16.8 , V$
Steps to Solve
- Calculate the base voltage (VB)
The base voltage can be found using the voltage divider rule. The formula for the base voltage is:
$$ V_B = V_{CC} \cdot \frac{R_E}{R_B + R_E} $$
Given that $V_{CC} = 20.7 , V$, $R_B = 500 , k\Omega$, and $R_E = 1 , k\Omega$:
$$ V_B = 20.7 \cdot \frac{1 , k\Omega}{500 , k\Omega + 1 , k\Omega} $$
- Calculate the emitter voltage (VE)
The emitter voltage can be found using the following equation, which includes the base-emitter voltage drop:
$$ V_E = V_B - V_{BE} $$
Given $V_{BE} = 0.7 , V$:
$$ V_E = V_B - 0.7 $$
- Calculate the emitter current (IE)
Using Ohm's Law, the emitter current can be derived from the emitter voltage and the emitter resistor:
$$ I_E = \frac{V_E}{R_E} $$
Given $R_E = 1 , k\Omega$, calculate $I_E$ using the previously found $V_E$.
- Calculate the collector current (IC)
The relationship between the collector current and emitter current can be represented as:
$$ I_C = \beta \cdot I_B $$
Also, since $I_E = I_C + I_B$, we can express $I_B$ in terms of $I_E$:
$$ I_B = \frac{I_E}{\beta + 1} $$
- Calculate base current (IB)
Now substitute $I_E$ into the equation for $I_B$:
$$ I_B = \frac{I_E}{\beta + 1} $$
Use $\beta = 100$ for the calculation.
- Calculate the collector voltage (VC)
Finally, the collector voltage can be calculated using:
$$ V_C = V_{CC} - I_C \cdot R_C $$
Given that $R_C = 5 , k\Omega$, substitute $I_C$ to find $V_C$.
- Collector Current, $I_C \approx 19.6 , mA$
- Base Current, $I_B \approx 196 , \mu A$
- Collector Voltage, $V_C \approx 16.8 , V$
More Information
In transistor circuits, the collector current, base current, and collector voltage are essential for understanding the transistor's operation in amplification or switching applications. The calculations show how the varying resistance and voltage influence the transistor's performance.
Tips
- Forgetting to account for the base-emitter voltage drop ($V_{BE}$) when calculating $V_E$.
- Misapplying the voltage divider rule or using incorrect resistor values.
- Not properly converting units (e.g., using mA instead of µA or kΩ without conversion).
AI-generated content may contain errors. Please verify critical information