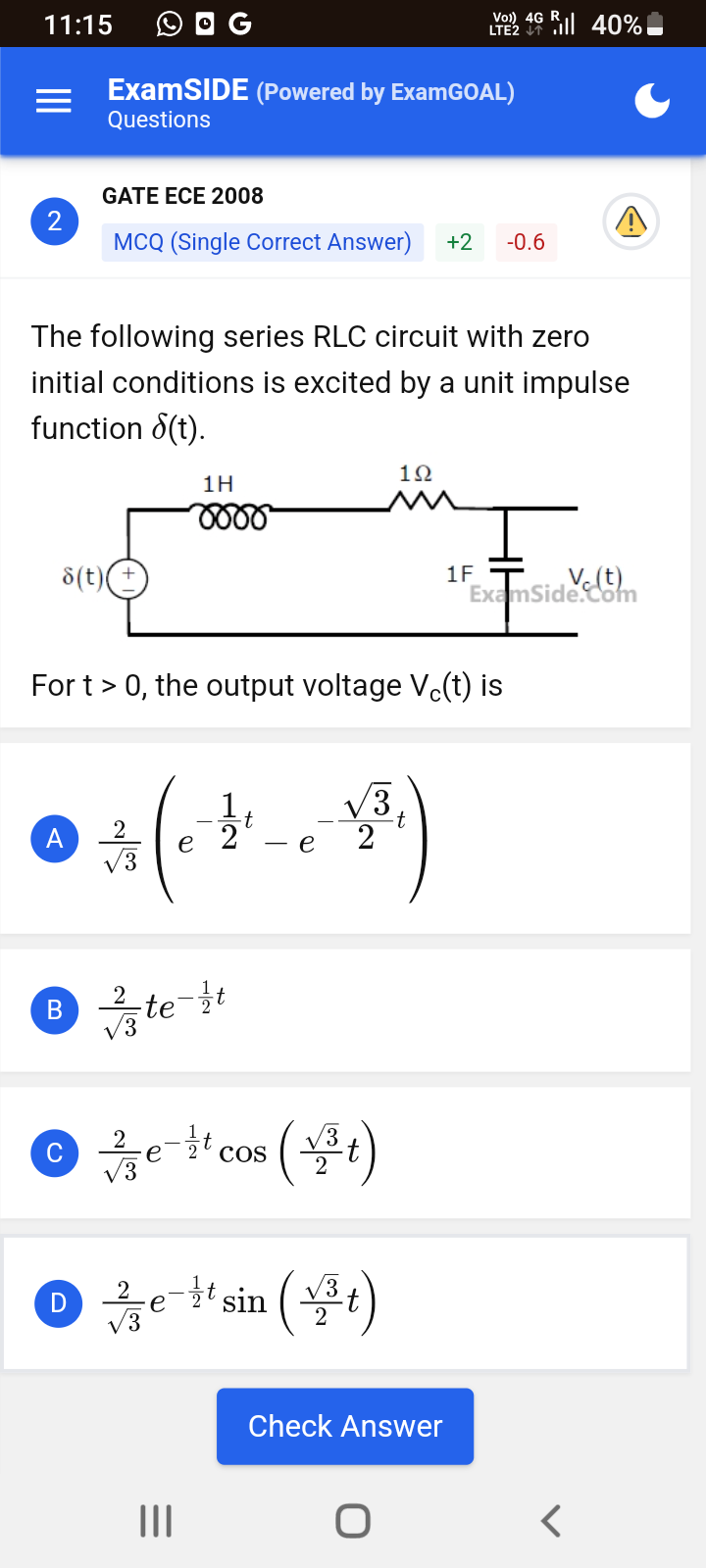
For t > 0, what is the output voltage Vc(t) of the series RLC circuit excited by a unit impulse function δ(t)?

Steps to Solve

1. Identify the Circuit Parameters

The given RLC circuit consists of a resistor $R = 1 , \Omega$, an inductor $L = 1 , H$, and a capacitor $C = 1 , F$.

2. Determine the Characteristic Equation

The characteristic differential equation for a series RLC circuit can be expressed as:

$$ L \frac{d^2 V_c(t)}{dt^2} + R \frac{dV_c(t)}{dt} + \frac{1}{C} V_c(t) = 0 $$

Substituting the circuit values:

$$ \frac{d^2 V_c(t)}{dt^2} + V_c(t) = 0 $$

3. Find the Damping Factor

The damping factor $\zeta$ and natural frequency $\omega_0$ are given by:

$$ \omega_0 = \frac{1}{\sqrt{LC}} = \frac{1}{\sqrt{1 \cdot 1}} = 1 $$

Given that $R < 2\sqrt{L/C}$, this circuit is underdamped.

4. Write the Solution for Underdamped Response

The general solution for the underdamped response is:

$$ V_c(t) = e^{-\zeta \omega_0 t} \left( A \cos(\omega_d t) + B \sin(\omega_d t) \right) $$

Where $\omega_d = \omega_0 \sqrt{1 - \zeta^2}$. Since $\zeta = \frac{R}{2\sqrt{L/C}} = \frac{1}{2}$, we find:

$$ \omega_d = 1 \sqrt{1 - \left(\frac{1}{2}\right)^2} = \frac{\sqrt{3}}{2} $$

5. Apply Initial Conditions

Since the circuit is excited by a unit impulse, the initial conditions are:

$$ V_c(0) = 0 \quad \text{and} \quad \frac{dV_c(t)}{dt} \bigg|_{t=0} = 1 $$

6. Solve for Coefficients A and B

We substitute the values into the general solution and apply the initial conditions:

$$ V_c(t) = e^{-\frac{1}{2} t} \left( A \cos\left(\frac{\sqrt{3}}{2}t\right) + B \sin\left(\frac{\sqrt{3}}{2}t\right) \right) $$

7. Find the Final Expression

After substituting initial conditions, we can derive that the output voltage $V_c(t)$ takes the form. The coefficient values are determined to give us one of the proposed answers.