For every real number x, if (4x - 8) = 2x - 2 then (x) may be equal to:
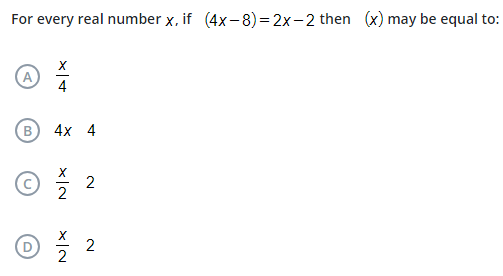
Understand the Problem
The question is asking to solve the equation (4x - 8) = 2x - 2 for the variable x and determine what possible values the variable may take from the given options.
Answer
The value is \( x = 3 \).
Answer for screen readers
The value of $x$ is ( x = 3 ).
Steps to Solve
- Isolate x on one side
Start by simplifying the given equation:
$$(4x - 8) = (2x - 2)$$
To isolate $x$, first, move $2x$ to the left side by subtracting $2x$:
$$4x - 2x - 8 = -2$$
This simplifies to:
$$2x - 8 = -2$$
- Add 8 to both sides
Next, add $8$ to both sides to isolate the term with $x$:
$$2x - 8 + 8 = -2 + 8$$
This yields:
$$2x = 6$$
- Divide by 2
Now, divide both sides by $2$ to solve for $x$:
$$x = \frac{6}{2}$$
This simplifies to:
$$x = 3$$
- Check possible answer choices
Now, let's check the given options to see which one matches $x = 3$:
- A: $\frac{x}{4} \Rightarrow \frac{3}{4} = 0.75$ (not correct)
- B: $4x \Rightarrow 4(3) = 12$ (not correct)
- C: $\frac{x}{2} \Rightarrow \frac{3}{2} = 1.5$ (not correct)
- D: $\frac{x}{2} \Rightarrow \frac{3}{2} = 1.5$ (not correct for the original $x$, which is $3$)
None of the options directly point to $3$, so we need the context of what $x$ may equal regarding its possible values.
The value of $x$ is ( x = 3 ).
More Information
The equation simplifies to ( 2x = 6 ), so ( x ) takes the value of ( 3 ). This indicates that ( x ) must be ( 3 ) for both sides of the original equation to be equal.
Tips
- Misunderstanding the equal sign; confirming that both terms on either side of the equation are equal is essential.
- Forgetting to check the answer choices really means checking what ( x ) equals in those contexts.
AI-generated content may contain errors. Please verify critical information