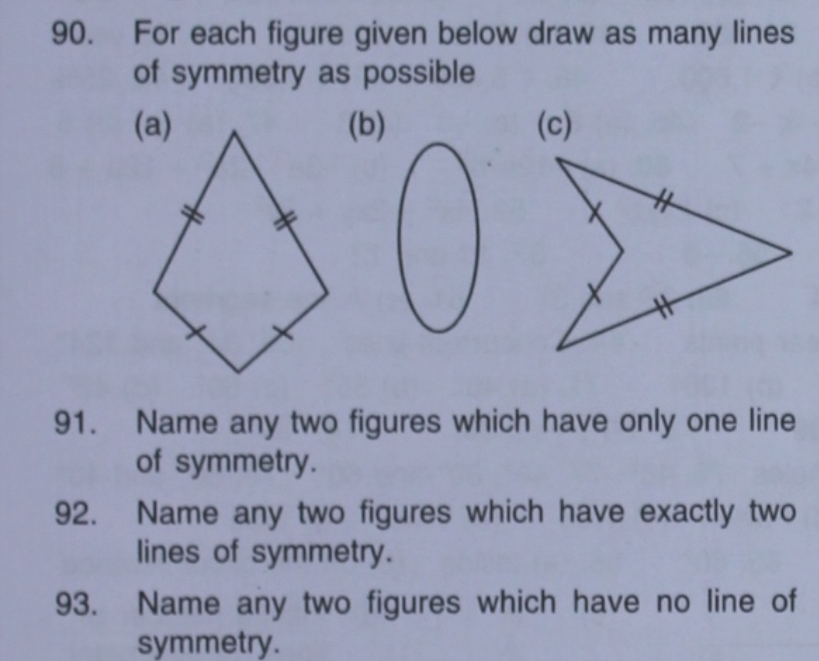
For each figure given below, draw as many lines of symmetry as possible. Name any two figures which have only one line of symmetry. Name any two figures which have exactly two line... For each figure given below, draw as many lines of symmetry as possible. Name any two figures which have only one line of symmetry. Name any two figures which have exactly two lines of symmetry. Name any two figures which have no line of symmetry.
Understand the Problem
The question is asking for an analysis of geometric figures to identify their lines of symmetry and to categorize different shapes based on the number of lines of symmetry they possess.
Answer
90. (a) 2, (b) Infinite, (c) 1 91. Right triangle, Scalene triangle 92. Rectangle, Kite 93. Irregular quadrilateral, Scalene triangle
Answer for screen readers
(a) 2 lines of symmetry
(b) Infinite lines of symmetry
(c) 1 line of symmetry (assuming it is isosceles)
- Right triangle, Scalene triangle
- Rectangle, Kite
- Irregular quadrilateral, Scalene triangle
Steps to Solve
-
Identify Lines of Symmetry for Each Figure
-
Figure (a): A diamond shape (or rhombus) has 2 lines of symmetry. Draw one line from the top vertex to the bottom vertex and another from the left vertex to the right vertex.
-
Figure (b): An oval (or ellipse) has an infinite number of lines of symmetry. You can draw any vertical, horizontal, or diagonal line through the center for symmetry.
-
Figure (c): A triangle can vary in types. An equilateral triangle has 3 lines of symmetry, drawn from each vertex to the midpoint of the opposite side. However, if this triangle is not equilateral, it may have only 1 line of symmetry depending on its shape. Here, let's assume it's isosceles, thus it has 1 line of symmetry from the top vertex to the midpoint of the base.
-
-
List Figures with Specific Lines of Symmetry
-
For Question 91, figures with only 1 line of symmetry:
- Example: A right triangle and a scalene triangle.
-
For Question 92, figures with exactly 2 lines of symmetry:
- Example: A rectangle and a kite.
-
For Question 93, figures with no line of symmetry:
- Example: An irregular quadrilateral and a scalene triangle.
-
(a) 2 lines of symmetry
(b) Infinite lines of symmetry
(c) 1 line of symmetry (assuming it is isosceles)
- Right triangle, Scalene triangle
- Rectangle, Kite
- Irregular quadrilateral, Scalene triangle
More Information
Lines of symmetry are the lines that divide a figure into two mirror-image halves. Regular shapes generally have more lines of symmetry than irregular shapes. For example, circles have infinite lines of symmetry, while most irregular polygons have none.
Tips
- Confusing types of triangles. Ensure to identify if a triangle is equilateral, isosceles, or scalene, as this affects its lines of symmetry.
- Miscounting lines of symmetry; take time to visualize or draw them out for complex shapes.
