For any three events A, B and C, show that: (i) P(A ∪ B | C) = P(A | C) + P(B | C) - P(A ∩ B | C) (ii) P(A ∩ B̅ | C) = P(A | C) - P(B | C) - P(A ∩ B | C)

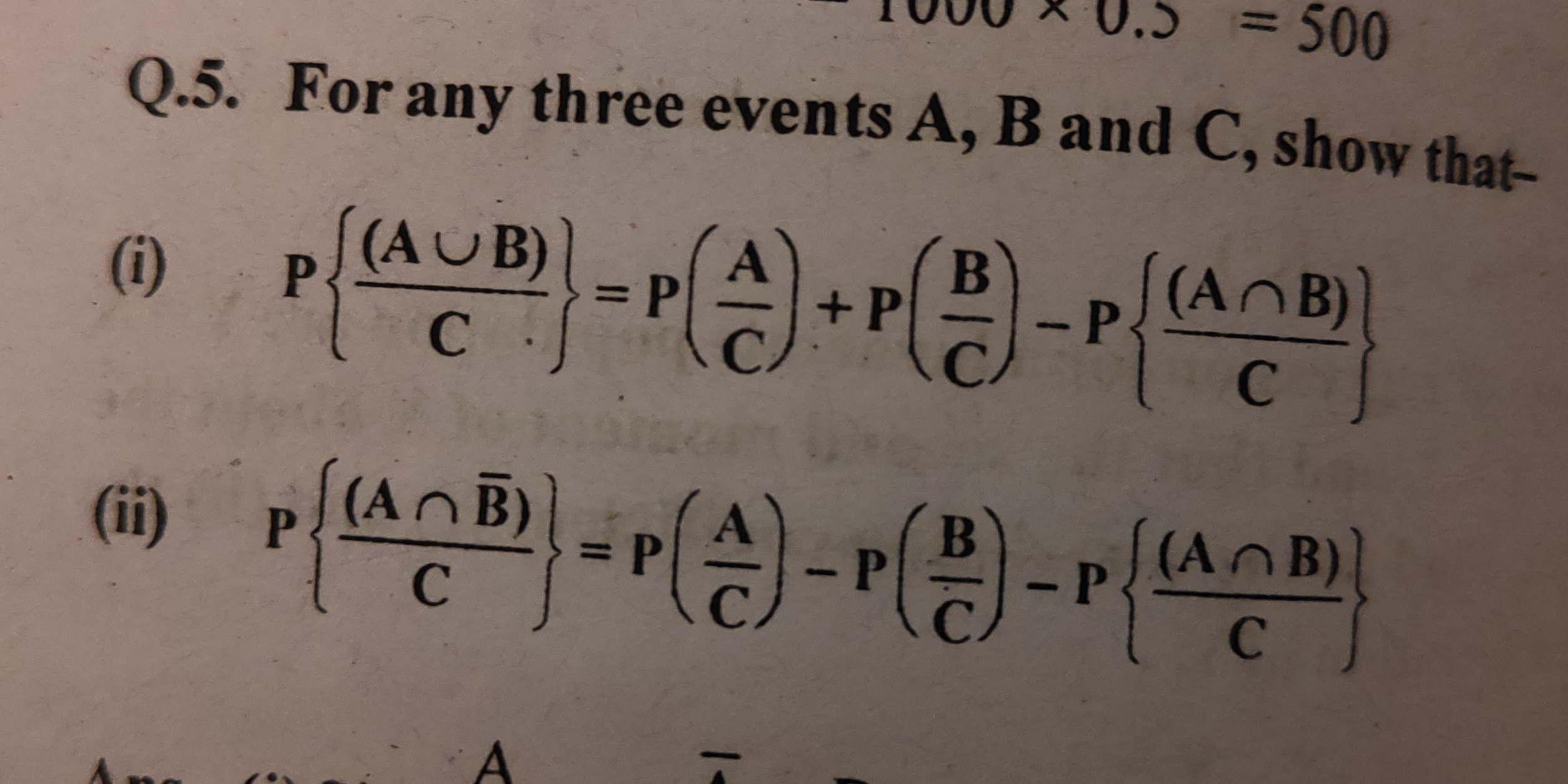
Understand the Problem

The question is asking to prove two probability equations involving three events A, B, and C. The first equation is about the probability of the union of A and B given C, while the second one involves the intersection of A and the complement of B given C.

Answer

(i) $$ P(A \cup B | C) = P(A | C) + P(B | C) - P(A \cap B | C) $$ (ii) $$ P(A \cap B̅ | C) = P(A | C) - P(B | C) - P(A \cap B | C) $$

Steps to Solve

Understanding Conditional Probability Conditional probability is defined as $$ P(A | C) = \frac{P(A \cap C)}{P(C)} $$ This can be applied to our events A, B, and C.
Using the Definition for Union of Events For the first equation, we know from the property of probability: $$ P(A \cup B | C) = P(A | C) + P(B | C) - P(A \cap B | C) $$ This can be derived using the definition of conditional probability. So, if we express $P(A \cup B | C)$ in terms of conditional probabilities: $$ P(A \cup B | C) = \frac{P((A \cup B) \cap C)}{P(C)} $$
Expanding the Left Side Expanding $(A \cup B) \cap C$ gives us: $$ (A \cup B) \cap C = (A \cap C) \cup (B \cap C) $$ Thus, $$ P((A \cup B) \cap C) = P((A \cap C) \cup (B \cap C)) $$
Using the Union Formula Using the probability formula for the union of two events: $$ P((A \cap C) \cup (B \cap C)) = P(A \cap C) + P(B \cap C) - P(A \cap B \cap C) $$ Applying the definition of conditional probability, this becomes: $$ P(A \cup B | C) \times P(C) = P(A | C) \times P(C) + P(B | C) \times P(C) - P(A \cap B | C) \times P(C) $$
Dividing by P(C) Cancelling $P(C)$ from all terms, we get: $$ P(A \cup B | C) = P(A | C) + P(B | C) - P(A \cap B | C) $$
Deriving the Second Equation For the second equation, we start with: $$ P(A \cap B̅ | C) = P(A | C) - P(A \cap B | C) $$ Using the fact that: $$ P(B | C) = P(A | C) - P(A \cap B | C) $$ leads us to: $$ P(A \cap B̅ | C) = P(A | C) - P(B | C) $$
Final Rearrangement Rearranging gives: $$ P(A \cap B̅ | C) = P(A | C) - P(B | C) - P(A \cap B | C) $$

(i) $$ P(A \cup B | C) = P(A | C) + P(B | C) - P(A \cap B | C) $$

(ii) $$ P(A \cap B̅ | C) = P(A | C) - P(B | C) - P(A \cap B | C) $$

More Information

The equations shown are fundamental properties of probabilities, especially useful in various fields like statistics and data analysis. They demonstrate how to handle combined probabilities and their intersections or unions under conditions.

Tips

Confusing the symbols for union ($\cup$) and intersection ($\cap$).
Forgetting to apply conditional properties correctly; conditional probabilities require careful consideration of the conditions involved.
Not simplifying the expressions adequately which can lead to incorrect assumptions.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!