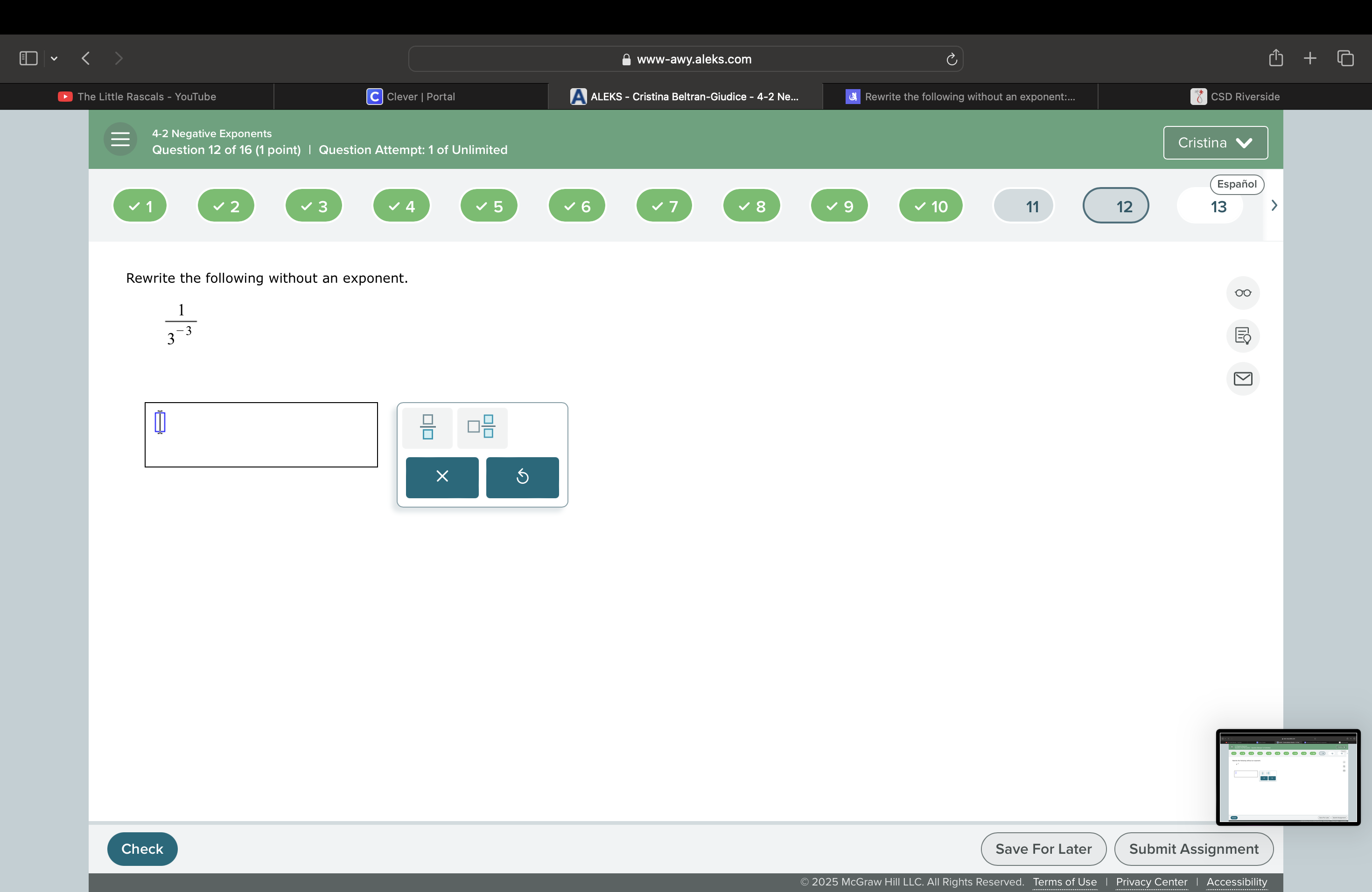
Rewrite the following without an exponent: 1/(3^(-3))
Understand the Problem
The question is asking to rewrite the expression 1/(3^(-3)) without using exponents. This involves applying the rules of exponents to simplify the expression.
Answer
27
Answer for screen readers
27
Steps to Solve
- Recognize negative exponent rule
A negative exponent means that the base can be expressed as a reciprocal. For any base $a$, $a^{-n} = \frac{1}{a^n}$. Thus, we can rewrite $3^{-3}$ as $\frac{1}{3^3}$.
- Rewrite the expression
Starting with the given expression:
$$ \frac{1}{3^{-3}} $$
Substituting the negative exponent with its reciprocal:
$$ \frac{1}{3^{-3}} = \frac{1}{\frac{1}{3^{3}}} $$
- Simplify the fraction
When simplifying a fraction $\frac{a}{\frac{1}{b}}$, it becomes $a \cdot b$. Applying this to our expression:
$$ \frac{1}{\frac{1}{3^{3}}} = 1 \cdot 3^{3} $$
Thus, we have:
$$ 3^{3} $$
- Calculate the final result
Now, calculate $3^3$:
$$ 3^3 = 3 \times 3 \times 3 = 27 $$
The expression without exponents is:
$$ 27 $$
27
More Information
The final answer, 27, is derived from simplifying the expression using the properties of exponents. The expression originally involved rewriting a base with a negative exponent into a reciprocal form, leading to a calculable positive expression.
Tips
- Confusing negative exponents with simply inverting the base. It’s essential to apply the negative exponent rule properly.
- Forgetting to actually compute the value after simplification.
AI-generated content may contain errors. Please verify critical information