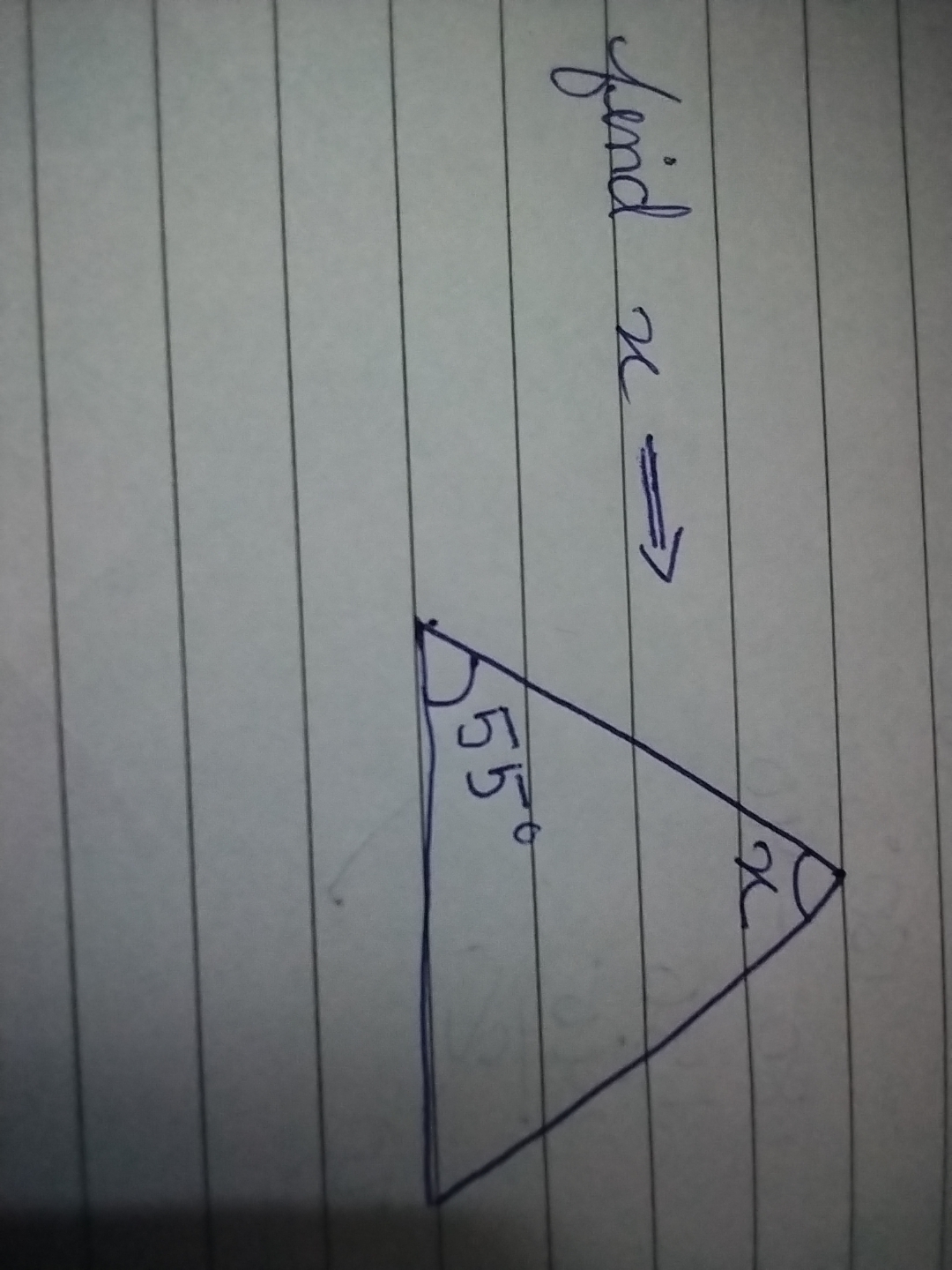
Find x in the triangle where one angle is 55 degrees.

Steps to Solve

1. Understanding the Triangle Angle Sum Property

The sum of all angles in a triangle equals 180 degrees.

2. Identifying Known Angles

We know one angle measures 55 degrees. Denote the unknown angle as $x$.

3. Setting Up the Equation

We can express the relationship using the angle sum property:

$$ 55 + x + y = 180 $$

Here, $y$ represents the third angle.

4. Finding the Value of the Third Angle (y)

To find $y$, we rearrange the equation:

$$ y = 180 - 55 - x $$

5. Determining the Unknown Angle x

Since we only need to find angle $x$, we can use the fact that the two other angles will also add up to form a triangle. However, if $y$ were another known angle, we could proceed to solve for $x$. In this case, we don't have $y$. Assuming $x$ is the other angle, we can conclude by using the remaining angle's constraint which often is that both $x$ and $y$ must also be defined as supplementary to 55 degrees, i.e.,

$$ x + 55 = 180 $$

So,

$$ x = 180 - 55 $$

6. Calculating x

Now compute the value:

$$ x = 125 $$