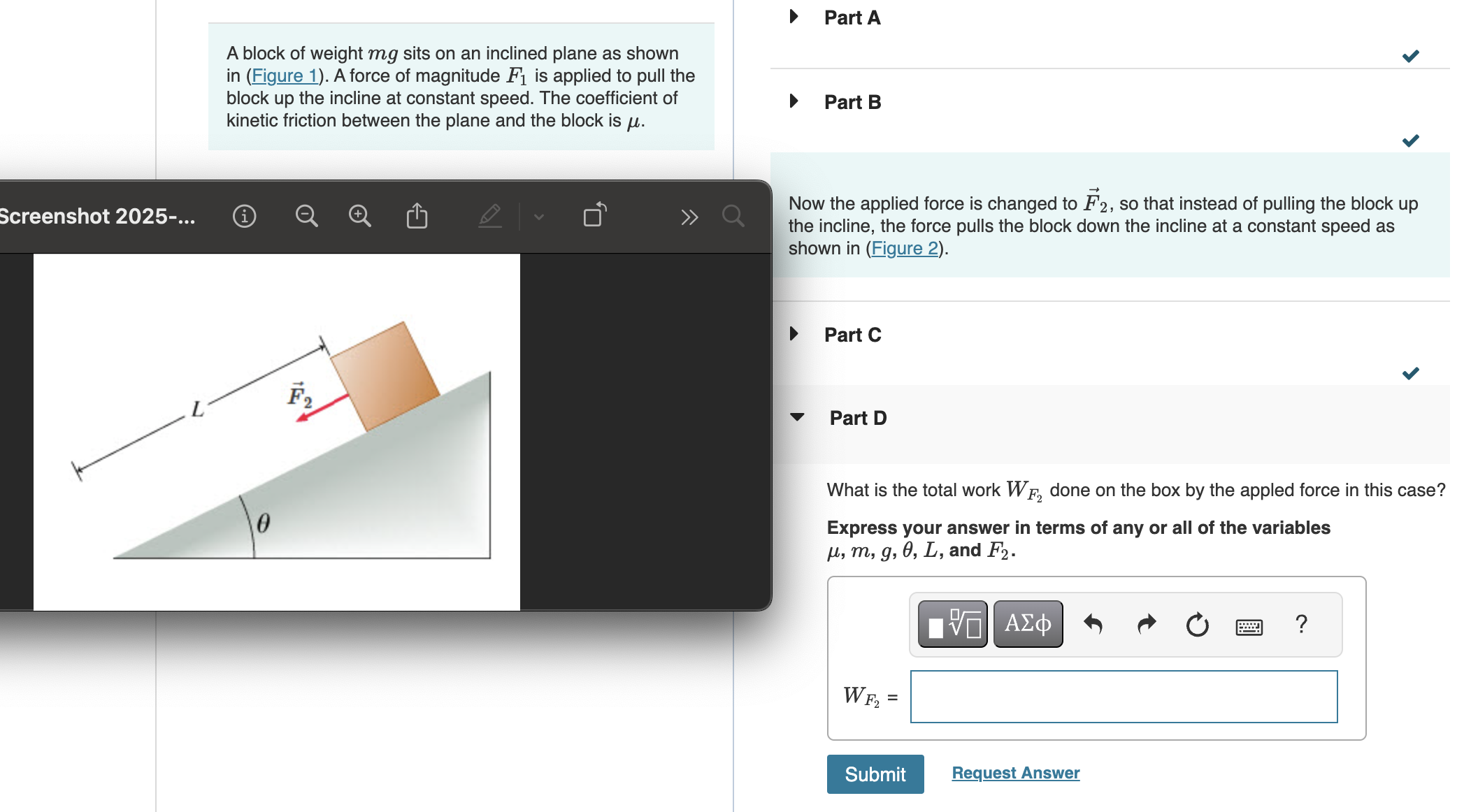
What is the total work W_{F2} done on the box by the applied force in this case? Express your answer in terms of any or all of the variables μ, m, g, θ, L, and F_{2}.
Understand the Problem
The question is asking for the total work done on a box by an applied force as it moves down an inclined plane at a constant speed. We need to express the answer in terms of various physical variables involved in the scenario.
Answer
$$ W_{F_2} = (mg \sin(\theta) + \mu (mg \cos(\theta))) L $$
Answer for screen readers
$$ W_{F_2} = (mg \sin(\theta) + \mu (mg \cos(\theta))) L $$
Steps to Solve
- Identify the forces acting on the box The forces acting on the block on the inclined plane include:
- The gravitational force: $F_g = mg$
- The normal force: $N$
- The frictional force: $F_f = \mu N$
- The applied force: $F_2$
-
Calculate the normal force The normal force can be calculated using the angle of the incline $\theta$: $$ N = mg \cos(\theta) $$
-
Determine the frictional force Using the normal force: $$ F_f = \mu N = \mu (mg \cos(\theta)) $$
-
Write down the net force acting on the box Since the block is moving at constant speed, the net force is zero: $$ F_2 - F_g \sin(\theta) - F_f = 0 $$
-
Express the total work done by the force $F_2$ The work done by the applied force as the block moves distance $L$ down the incline can be expressed as: $$ W_{F_2} = F_2 \cdot L $$
-
Substitute the expressions for forces Substituting the expression of gravitational and frictional forces into the equilibrium equation, we find: $$ F_2 = mg \sin(\theta) + \mu (mg \cos(\theta)) $$
-
Substituting this back into the work done Now substituting this value of $F_2$ into the work equation: $$ W_{F_2} = (mg \sin(\theta) + \mu (mg \cos(\theta))) L $$
$$ W_{F_2} = (mg \sin(\theta) + \mu (mg \cos(\theta))) L $$
More Information
The work done by the applied force $W_{F_2}$ takes into account both the gravitational component along the incline and the frictional force opposing the motion. This equation combines fundamental concepts of dynamics and work-energy theorem.
Tips
- Forgetting to consider the direction of forces along the incline.
- Not accounting for the frictional force correctly; ensure to use the correct formula.
- Assuming that the normal force is equal to the weight without considering the incline angle.
AI-generated content may contain errors. Please verify critical information