Find the volume of the wedge cut from the first octant by the cylinder z = 12 - 3y^2 and the plane x + y = 2.
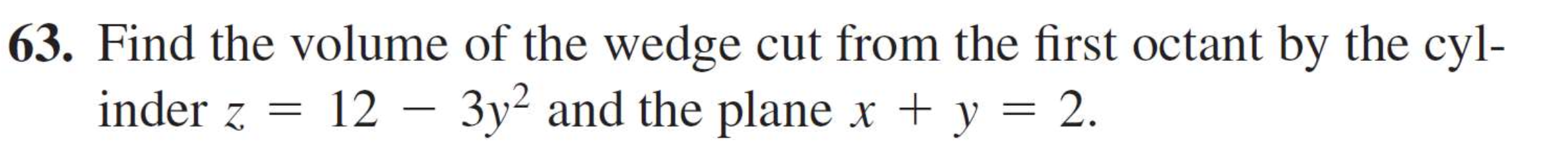
Understand the Problem
The question is asking to calculate the volume of a specific geometric shape, defined as a wedge cut from the first octant by a cylinder and a plane. This involves using concepts from calculus and geometry to find the volume within the specified constraints.
Answer
The volume of the wedge is \( V = 20 \).
Answer for screen readers
The volume of the wedge is given by ( V = 20 ).
Steps to Solve
- Identify the boundaries for (x) and (y)
The plane (x + y = 2) limits the region in the (xy)-plane. We can express (x) in terms of (y): $$ x = 2 - y $$ Since we are in the first octant, both (x) and (y) must be non-negative. Thus, (0 \leq y \leq 2).
- Determine the limits for (z)
The volume is bounded above by the surface defined by the equation of the cylinder: $$ z = 12 - 3y^2 $$ This determines the height of the volume above any point ((x,y)) in the specified region.
- Set up the integral for the volume
The volume (V) can be calculated using a double integral: $$ V = \int_0^2 \int_0^{2-y} (12 - 3y^2) , dx , dy $$ Here, (x) ranges from (0) to (2 - y) and (y) ranges from (0) to (2).
- Evaluate the inner integral
First, integrate with respect to (x): $$ \int_0^{2-y} (12 - 3y^2) , dx = (12 - 3y^2) \cdot (2 - y) $$ This expands to: $$ = (12 - 3y^2)(2 - y) = 24 - 12y - 6y^2 + 3y^3 $$
- Evaluate the outer integral
Now, integrate the result from the previous step with respect to (y): $$ V = \int_0^2 (24 - 12y - 6y^2 + 3y^3) , dy $$
- Calculate the integral
Calculating each term gives: $$ V = [24y - 6y^2 - 2y^3 + \frac{3}{4}y^4]_0^2 $$ Evaluating this from (0) to (2): $$ = [48 - 24 - 16 + 12] - [0] = 20 $$
The volume of the wedge is given by ( V = 20 ).
More Information
The resulting volume of (20) cubic units represents the space contained within the defined geometric constraints. The integration process used helps visualize how calculus can quantify irregular shapes and volumes.
Tips
- Forgetting to consider the limits of integration properly which can lead to incorrect volume calculations.
- Misapplying the order of integration or the boundaries set by the geometrical constraints.
AI-generated content may contain errors. Please verify critical information