Find the volume of the solid generated by revolving the region between the y-axis and the curve x = 2/y, 1 ≤ y ≤ 4, about the y-axis.
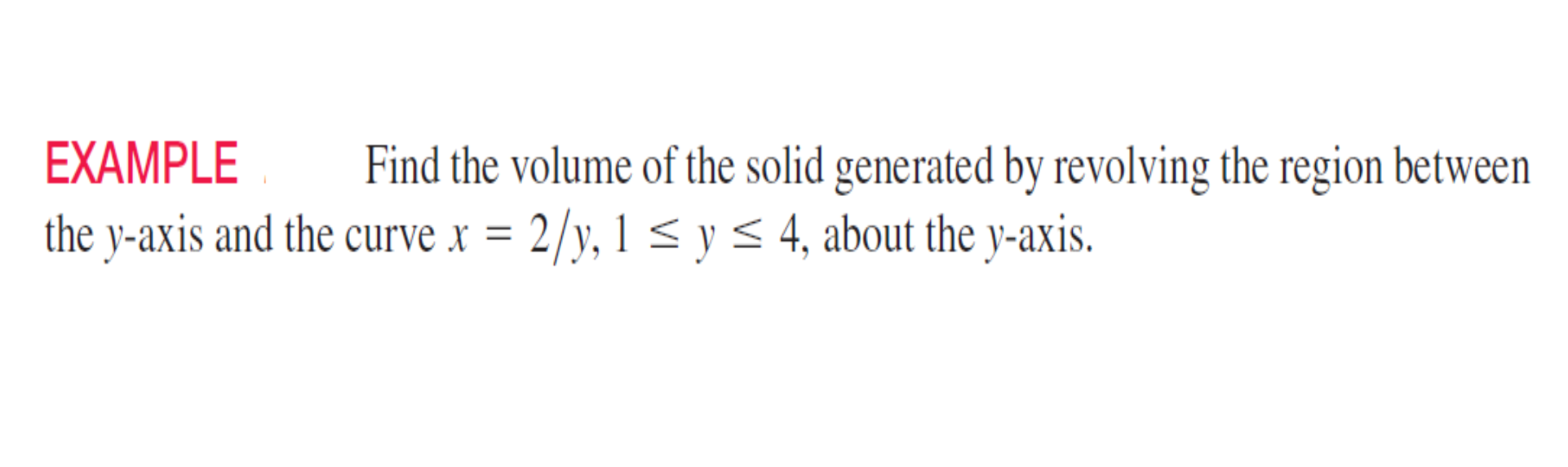
Understand the Problem
The question is asking for the volume of a solid formed by revolving a specific region around the y-axis. This involves calculus concepts related to volumes of revolution, specifically using the method suitable for functions defined in terms of y.
Answer
The volume of the solid is \( V = 3\pi \).
Answer for screen readers
The volume of the solid is ( V = 3\pi ).
Steps to Solve
- Identify the function and limits of integration
The curve is given by ( x = \frac{2}{y} ), which represents the radius of the solid when revolving around the y-axis. The limits of integration are from ( y = 1 ) to ( y = 4 ).
- Set up the volume integral
To find the volume ( V ) of the solid formed by revolving the area around the y-axis, we use the integral for the volume of revolution:
$$ V = \pi \int_{a}^{b} [f(y)]^2 , dy $$
In our case, ( f(y) = \frac{2}{y} ), therefore,
$$ V = \pi \int_{1}^{4} \left(\frac{2}{y}\right)^2 , dy $$
- Simplify and compute the integral
First, simplify ( \left(\frac{2}{y}\right)^2 ):
$$ \left(\frac{2}{y}\right)^2 = \frac{4}{y^2} $$
Now substitute this back into the volume integral:
$$ V = \pi \int_{1}^{4} \frac{4}{y^2} , dy $$
- Evaluate the integral
To evaluate ( \int \frac{4}{y^2} , dy ), we can rewrite it as:
$$ \int \frac{4}{y^2} , dy = 4 \int y^{-2} , dy $$
The integral of ( y^{-2} ) is:
$$ -\frac{4}{y} $$
Thus,
$$ V = \pi \left[-\frac{4}{y}\right]_{1}^{4} $$
Now substitute the limits:
$$ V = \pi \left( -\frac{4}{4} + \frac{4}{1} \right) $$
- Simplify to find the final volume
Calculating the expression gives us:
$$ V = \pi \left( -1 + 4 \right) = \pi \cdot 3 = 3\pi $$
The volume of the solid is ( V = 3\pi ).
More Information
This problem illustrates the application of the disk method in calculus, which is used to find the volumes of solids of revolution. In this case, we found the volume formed by revolving a rectangular area defined by a curve and the y-axis.
Tips
- Forgetting to square the function inside the integral when setting up the volume formula.
- Incorrectly evaluating the definite integral limits.
- Not remembering to adjust the formula when rotating about the y-axis versus the x-axis.
AI-generated content may contain errors. Please verify critical information